O que é função?

Matemática

Ensino Médio

Reforço Escolar

Funções

Álgebra

Teoria dos Números

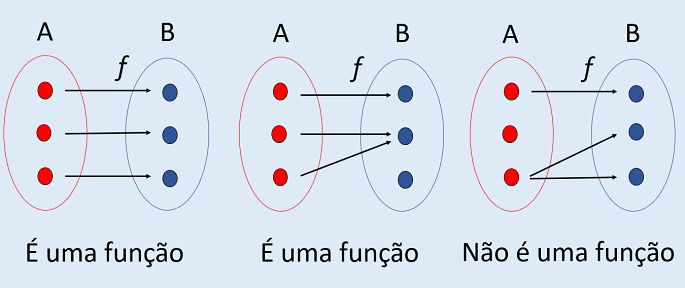
Na Matemática, função corresponde a uma associação dos elementos de dois conjuntos, ou seja, a função indica como os elementos estão relacionados.

Por exemplo, uma função de A em B significa associar cada elemento pertencente ao conjunto A a um único elemento que compõe o conjunto B, sendo assim, um valor de A não pode estar ligado a dois valores de B.

definição de função

Notação para função: f: A → B (lê-se: f de A em B).

Representação das funções

Em uma função f: A → B o conjunto A é chamado de domínio (D) e o conjunto B recebe o nome de contradomínio (CD).

Um elemento de B relacionado a um elemento de A recebe o nome de imagem pela função. Agrupando todas as imagens de B temos um conjunto imagem, que é um subconjunto do contradomínio.

Exemplo: observe os conjuntos A = {1, 2, 3, 4} e B = {1, 2, 3, 4, 5, 6, 7, 8}, com a função que determina a relação entre os elementos f: A → B é x → 2x. Sendo assim, f(x) = 2x e cada x do conjunto A é transformado em 2x no conjunto B.

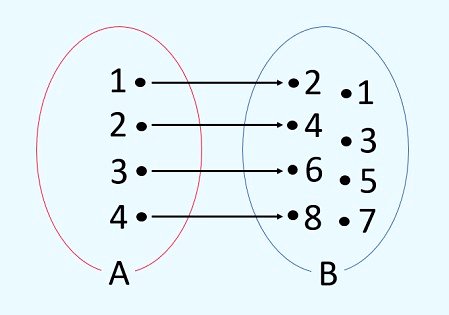
Representação de uma função

Note que o conjunto de A {1, 2, 3, 4} são as entradas, "multiplicar por 2" é a função e os valores de B {2, 4, 6, 8}, que se ligam aos elementos de A, são os valores de saída.

Portanto, para essa função:

O domínio é {1, 2, 3, 4}
O contradomínio é {1, 2, 3, 4, 5, 6, 7, 8}
O conjunto imagem é {2, 4, 6, 8}

Tipos de funções

As funções recebem classificações de acordo com suas propriedades. Confira a seguir os principais tipos.

Função sobrejetora

Na função sobrejetora, o contradomínio é igual ao conjunto imagem. Portanto, todo elemento de B é imagem de pelo menos um elemento de A.

Notação: f: A → B, ocorre a Im(f) = B

Exemplo:

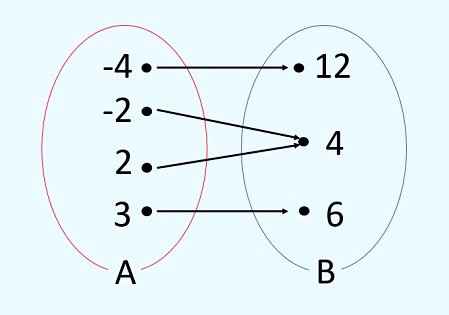
exemplo de função sobrejetora

Para a função acima:

O domínio é {-4, -2, 2, 3}
O contradomínio é {12, 4, 6}
O conjunto imagem é {12, 4, 6}

Função injetora

Na função injetora, todos os elementos de A possuem correspondentes distintos em B e nenhum dos elementos de A compartilham de uma mesma imagem em B. Entretanto, podem existir elementos em B que não estejam relacionados a nenhum elemento de A.

Exemplo:

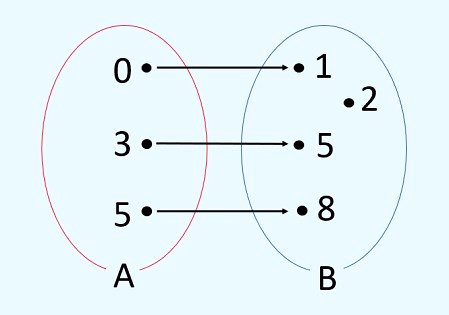
exemplo de função injetora

Para a função acima:

O domínio é {0, 3, 5}
O contradomínio é {1, 2, 5, 8}
O conjunto imagem é {1, 5, 8}

Função bijetora

Na função bijetora , os conjuntos apresentam o mesmo número de elementos relacionados. Essa função recebe esse nome por ser ao mesmo tempo injetora e sobrejetora.

Exemplo:

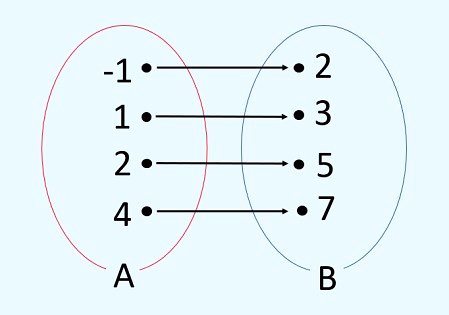
Exemplo de função bijetora

Para a função acima:

O domínio é {-1, 1, 2, 4}
O contradomínio é {2, 3, 5, 7}
O conjunto imagem é {2, 3, 5, 7}

Função inversa

A função inversa, é um tipo de função bijetora, por isso é sobrejetora e injetora ao mesmo tempo.

Através desse tipo de função é possível criar novas funções ao inverter os elementos.

Função par

Uma função é par quando f(-x) = f(x). Assim a função possui a mesma imagem, tanto para x quanto para -x.

Função ímpar

Uma função é ímpar quando f(-x) = -f(x). O gráfico de uma função ímpar é simétrico em relação à origem.

Função composta

A função composta, é um tipo de função matemática que combina duas ou mais variáveis.

Duas funções, f e g, podem ser representadas como função composta por:

fog (x) = f(g(x))
gof (x) = g(f(x))

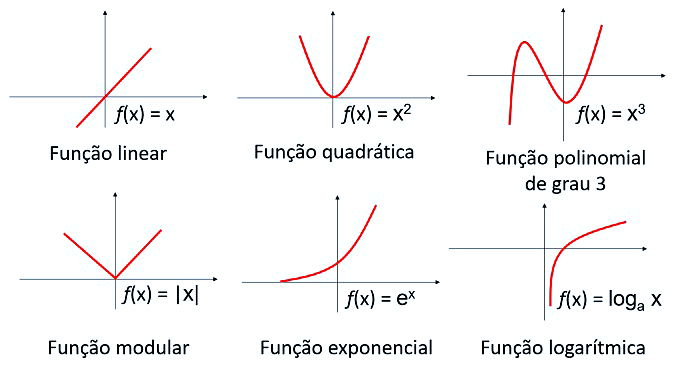
Função modular

A fução modular, associa elementos em módulos e seus números são sempre positivos.

$reto f parêntese esquerdo reto x parêntese direito espaço igual a espaço linha vertical reto x linha vertical espaço igual a espaço chaveta esquerda atributos de tabela alinhamento de coluna left fim dos atributos linha com célula com reto x vírgula espaço para espaço reto x maior ou igual a 0 fim da célula linha com célula com menos reto x vírgula espaço para espaço reto x menor que 0 fim da célula fim da tabela$

Função afim

A função afim,, também chamada de função do 1º grau, apresenta uma taxa de crescimento e um termo constante.

f(x) = ax + b

a: coeficiente angular
b: coeficiente linear

Função linear

A função linear é um caso particular da função afim, sendo definida como f(x) = ax.

Quando o valor do coeficiente (a) que acompanha o x da função for igual a 1, a função linear é uma função identidade.

Função quadrática

A função quadrática, é também chamada de função do 2º grau.

f(x) = ax²+ bx + c, sendo a ≠ 0

a, b e c: coeficientes da função polinomial de grau 2.

Função logarítmica

A função logaritmica de base a é representada por f(x) = log_ax, sendo a real positivo e a ≠ 1.

Ao invertermos a função logarítmica passamos a ter uma função exponencial.

Função exponencial

A função exponencial apresenta uma variável no expoente e a base é sempre maior que zero e diferente de um.

f(x) = a^x, sendo a > 0 e a ≠ 0

Função polinomial

A função polinomial é definida por expressões polinomiais.

f(x) = a_n . xⁿ + a_{n – 1} . x^{n – 1}+ ...+a₂. x² + a₁ . x + a₀

a_n, a_n-1, ... , a₂, a₁, a₀: números complexos
n: número inteiro
x: variável complexa

Funções trigonométricas

As funções trigonométricas estão relacionadas com as voltas no ciclo trigonométrico, como:

Função Seno: f(x) = sen x
Função Cosseno:f(x) = cos x
Função Tangente: f(x) = tg x

Gráfico de uma função

A maneira como um elemento y se relaciona com um elemento x é expressa através de um gráfico, que nos dá a ideia do comportamento da função.

Cada ponto no gráfico é dado por um par ordenado de x e y, onde x é o valor de entrada e y é o resultado da relação definida pela função, ou seja, x → função → y.

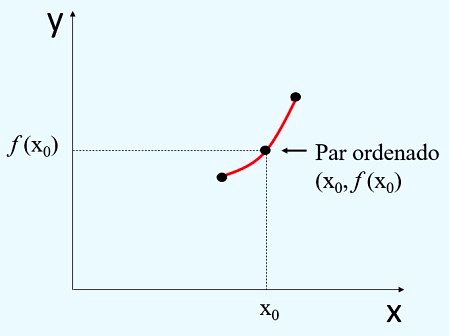
Exemplo de gráfico

Para construir um gráfico, cada elemento x da função deve ser inserido no eixo horizontal (abcissas) e os elementos y são posicionados no eixo vertical (ordenadas).

Os possíveis valores de x formam o conjunto Domínio. Já o conjunto dos valores assumidos por y, formam o conjunto imagem.

Confira alguns exemplos de gráficos de funções.

gráficos de funções