Aulas particulares Tarefas Minerva IA Entrar Criar conta

Desafios & Mistérios da Matemática (Conjuntos Numéricos)

05/03/15

Profes / Blog / Matemática

Números Complexos Conjuntos Teoria dos Números Geral Operações Ensino Fundamental Programação em R Ensino Médio

Bom Dia, Turma!

Conjuntos Numéricos é um tópico da matemática que eu classifico como fundamental, pois ele se estende para todos os campos da Exatas (Física, Química, Computação e etc.) e ao nosso Cotidiano (Por Exemplo, quando pedidos uma duzia de ovos; meio quilo de carne ou até mesmo quando medimos a circunferência da cintura), sendo assim, é de suma importância entendermos os conceitos e as notações utilizadas para classificar tais conjuntos.

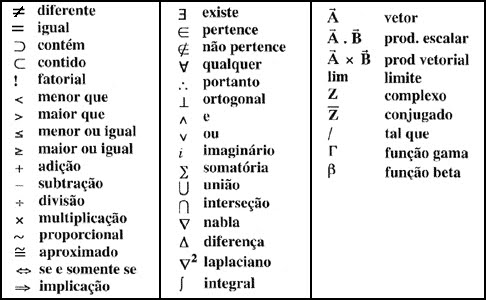
Simbologia

* (asterisco) sobrescrito ao simbolo do conjunto numérico significa que excluimos o zero do conjunto.

+ (positivo) subescrito ao simbolo do conjunto numérico significa que excluimos os números negativos do conjunto.

- (negativo) subescrito ao simbolo do conjunto numérico significa que excluimos os números positivos do conjunto.

Conjunto dos Números Naturais ( $\mathbb{N}$ )

O conjunto dos números Naturais é forma pelos números inteiros não-negativos.

Na Integra:

$\mathbb{N}$ = {0, 1, 2, 3, ...}

Resolva exercícios e atividades acadêmicas

Envie atividades, projetos ou exercícios para um professor resolver no seu prazo.

Não incluindo o zero:

$\mathbb{N}^*$ = {1, 2, 3, ...} ou $\mathbb{N}$ - {0} ou { X ∈ $\mathbb{N}$ / X > 0 }

Conjunto dos Números Inteiros ( $\mathbb{Z}$ )

Os números inteiros são constituídos pelo conjunto dos números naturais (incluindo o zero) e os números negativos simétricos deste conjunto, isto é, opostos (não-positivos).

Na Integra:

Encontre o professor particular perfeito

$\mathbb{Z}$ = {..., -3, -2, -1, 0, 1, 2, 3, ...}

Não inclui o zero:

$\mathbb{Z}$ ^*= {..., -3, -2, -1, 1, 2, 3 ...} ou $\mathbb{Z}$ - {0} ou { X ∈ $\mathbb{Z}$ / X < 0 ou X > 0 }

Não inclui os números negativos simétricos (inteiros não-positivos):

Tutoria com Inteligência Artificial

Tecnologia do ChatGPT. Use texto, áudio, fotos, imagens e arquivos.

$\mathbb{Z}$ ₊ = {0, 1, 2, 3 ...} ou $\mathbb{Z}$ - $\mathbb{Z}$ _- ou { X ∈ $\mathbb{Z}$ / X ≥ 0 }

$\mathbb{Z}$ ₊ = $\mathbb{N}$

Não inclui os números naturais (inteiros não-negativos):

$\mathbb{Z}$ _- = {..., -1, -2, -3, 0} ou $\mathbb{Z}$ - $\mathbb{Z}$ + ou { X ∈ $\mathbb{Z}$ / X ≤ 0 }

Não inclui os números negativos simétricos e o zero (inteiros positivos):

$\mathbb{Z}$ ^*₊ = {1, 2, 3 ...} ou $\mathbb{Z}$ ^*- $\mathbb{Z}$ ^*_- ou { X ∈ $\mathbb{Z}$ / X > 0 }

$\mathbb{Z}$ ^*₊= $\mathbb{N}^*$

Não inclui os números naturais e o zero (inteiros negativos):

$\mathbb{Z}$ ^*_- = {..., -1, -2, -3} ou $\mathbb{Z}$ ^* - $\mathbb{Z}$ ^*+ ou { X ∈ $\mathbb{Z}$ / X < 0 }

Obs.: Dizemos números não-negativos ou não-positivos ao invés de negativos ou positivos pelo fato de o zero ser um elemento neutro.

Conjunto dos Números Racionais ( $\mathbb{Q}$ )

O conjunto dos Números Racionais é aquele, no qual, conseguimos expor um número em uma forma fracionária, isto é, na forma a/b. Para existir esta ocorrência é necessário que a ∈ $\mathbb{Z}$ e b ∈ $\mathbb{Z}$ ^*, ou seja, "a" poderá ser qualquer número inteiro e "b" qualquer número inteiro diferente de zero.

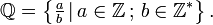
$\mathbb{Q}=\left\{\begin{matrix}\frac{a}{b}\end{matrix}\,|\,a\in\mathbb{Z}\,;\,b\in\mathbb{Z^{*}}\right\}.$

Na Integra:

$\mathbb{Q}$ = {..., -3/2, -2/3, -1, 0, 1/2, 7/9, √4, ...}

Não inclui o zero:

$\mathbb{Q}$ ^*= {...,3/2, -2/3, -1, 1/2, 7/9, √4...} ou $\mathbb{Q}$ - {0} ou { X ∈ $\mathbb{Q}$ / X < 0 ou X > 0 }

Não inclui os números inteiros não-positivos com pares ordenados (fração):

$\mathbb{Q}$ ₊ = {0, 1/2, 7/9, √4, ...} ou $\mathbb{Q}$ -_{$\mathbb{Q}$ -}ou { X ∈ $\mathbb{Q}$ / X ≥ 0 }

Não inclui os números inteiros não-negativos com pares ordenados (fracão):

_{$\mathbb{Q}$ -} = {..., -3/2, -2/3, -1, 0} ou $\mathbb{Q}$ - $\mathbb{Q}$ + ou { X ∈ $\mathbb{Q}$ / X ≤ 0 }

Não inclui os números negativos negativos com pares ordenados (fração)

$\mathbb{Q}$ ^*₊= {1/2, 7/9, √4, ...} ou $\mathbb{Q}$ ^*- $\mathbb{Q}$ ^*_- ou { X ∈ $\mathbb{Q}$ / X > 0 }

Não inclui os números negativos positivos com pares ordenados (fração)

$\mathbb{Q}$ ^*_- = {..., -3/2, -2/3, -1} ou $\mathbb{Q}$ ^* - $\mathbb{Q}$ ^*+ ou { X ∈ $\mathbb{Q}$ / X < 0 }

Obs.: É importante ressaltar que um numero inteiro {-2,-1,3,6} podem ser colocadas no formato de fração a/b, com b igual a 1.

Conjunto dos Números Irracionais ( $\mathbb{I}.$ )

Os números irracionais são aqueles números em que não conseguimos expor em forma fracionária, ou seja, dízima periódica simples ou composta. Exemplos de números que compõe esse conjunto são:

√2 = 1.4142135...

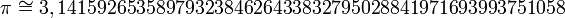$\pi \cong 3,1415926535897932384626433832795028841971693993751058$ ...

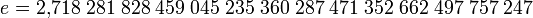$e=2{,}718\;281\;828\;459\;045\;235\;360\;287\;471\;352\;662\;497\;757\;247$ ...

Obs.: Os números irracionais não contemplam os conjuntos N, Z e Q; ele é um conjunto isolado que esta contido no conjunto dos Reais (R) que por sua vez esta contido no conjunto dos números complexos.

Conjunto dos Números Reais (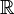 $\mathbb{R}\,$ )

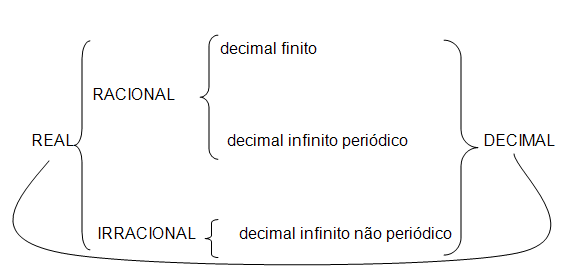
Os números Reais são aqueles que engloba todos os conjuntos acima, como definição podemos dizer que é o conjunto de todos os números que possui representação decimal exata, dízima periódica (números racionais) e representação decimal não exata, dízima não periódica (números irracionais).

Fonte: Estrutura esquematica extraida do site Objetivo (Conteúdo Online)

Obs.: É o conjunto que abrange todos os já mencionados, quando resolvemos uma equação ou sistema provavelmente a resposta esta neste conjunto.

Conjunto dos Números Complexos ( $\mathbb{C}$ )

O Conjunto dos números complexos veio para suprir uma necessidade matemática para raízes negativas, no qual matematicos se deparavam. Sendo assim um numero complexo (z) é composto de uma parte Real (x) e Imaginária (y).

$z = x + yi$

Unidade imaginária é reapresentada por i, sendo i = √-1.

Obs.: Diferente do que muitos pensam os números imaginários (i) existem, digamos que a escolha do nome não foi a melhor, pois induz a uma interpretação equivocada.

Representação Resumida e Esquematica dos Conjuntos Numéricos

$\mathbb{N}\sub\mathbb{Z}\sub\mathbb{Q}\sub\mathbb{R}\sub\mathbb{C}\sub\cdots$

Leitura: Naturais esta contido em Inteiros, que por sua vez esta contido em Racionais, que por sua vez esta contido em Reais e que por sua vez esta contido em Complexos.

Fonte: Imagem extraida do site Matematiquês

Fonte: Esquema extraido do site Virtual Escola

Desafio

Sabendo-se que √-2 é um número Complexo (C).

a) Converta o número acima em um númerio Inteiro (Z), Racional (Q) e Irracional (I) utilizando operações matemáticas com os números √-2 e √2.

b) Utilizando-se as operações matemáticas com o número acima e os números √-2 e √2, formou-se o seguinte conjunto, A = {0, 1/2, 2/3, √(1/2), 1, 2, 2√2, 3, √-1}, classifique na tabela abaixo os sub-conjuntos numérico com pertence (∈) e não pertence (∉).

Sub-Conjunto	N	Z	Q	I	R	C
{0,1}
{0,2/3,1/2}
{0,2/3}
{√(1/2), √-1}
{1,2,3}
{√(1/2),2√2}
{0,2√2}
{0}
{√-1}

c) Por qual número devemos multiplicar o número acima para se obter o número $\pi$ com uma casa decimal de precisão. Qual conjunto o número pertencia antes da mutiplicação e após?