Desafios & Mistérios da Matemática (Estatística Descritiva)

Bom dia Turma,

Definição de Estatística

A Estatística é um conjunto de técnicas que possibilita de uma forma sistemática, organizar, descrever, analisar e interpretar uma população e/ou amostra de uma determinada área do Conhecimento, como é o caso do Censo, IBOPE e muitas outras pesquisas de mercado.

Definição de Estatística Descritiva

É a primeira etapa da análise, no qual, abrange técnicas e métodos para descrever e resumir os dados.

Conceitos Básicos

População: Quando conhecemos o grupo como um todo, isto é, todos os elementos pertencentes ao mesmo. Ex.: Quantidade de Habiltantes de Uma Região, Número de Alunos de uma Classe e etc.

Amostra: É uma parte ou porção da população (sub-conjunto da população).

Variáveis Qualitativas: São aquelas que qualificam um grupo, ou seja, é uma característica e não um número.

-- Nominal: São aquelas que podemos nomear em um grupo (Ex.: Cor dos Olhos, Sexo, Religião, Time de Futebol e etc.)

-- Ordinal: São aquelas que podemos ordenar em um grupo (Ex.: Grau de Instrução, Classe Social e etc.)

Variáveis Quantitativas: São aquelas que extraímos um valor mensurável.

-- Continua: São aquelas medidas, no qual, podemos ter em sua extensão infinitos valores (Ex.: Peso, Comprimento, Tempo e etc.)

-- Discreta: São valores oriundos de quantidades finitas (Ex.: Numero de defeitos em máquinas, Número de filhos e etc.)

Variáveis Quantitativas

Medidas de Posição: Moda, Média, Mediana, Ponto Médio, Frequência, Separatrizes (Quartil, Percentil, Decis, Quintil)

Medidas de Dispersão: Amplitude Total, Desvio Padrão, Variância, Coeficiente de Variação

Medidas de Posição

Moda (mo)

É o valor que ocorre com maior frequência na amostra ou população, caso existam empates teremos mais de uma moda.

Exemplo:

{4, 1, 3, 8, 8, 8, 7, 9}

mo = 8

{4, 4, 5, 5, 7, 9, 1}

mo = 4 e 5 (bimodal)

Obs.: Para mais de dois empates chamamos de multimodal.

Média ( μ ou )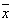

É a soma de todos os valores de uma população ou amostra dividido pelo nº de elementos (n),sendo assim, é a Média Aritmética.

Exemplo:

{4, 1, 3, 8, 8, 8, 7, 9}

= (4 + 1 + 3 + 8 + 8 + 8 + 7 + 9) / 7 = 48/8 = 6

x = 6

Obs.: Para representar uma média de uma população utilizamos o simbolo "μ" e para uma amostra "x".

Mediana (md)

É o valor central de uma amostra ou população de números ordenados (Rol)

-- Quantidade de números Impares

 Exemplo:

{4, 1, 3, 8, 8, 8, 7, 9, 11}

Ordenar

Rol = {1, 3, 4, 7, 8, 8, 8, 9, 11}

md = 8

-- Quantidade de números Pares

Exemplo:

{4, 1, 3, 8, 8, 8, 7, 9}

Ordenar

Rol = {1, 3, 4, 7, 8, 8, 8, 9}

md = (7+8)/2 =7,5

md = 7,5

Obs.: Rol é a ordenação crescente dos dados de um conjunto

Ponto Médio

Valor que esta no "meio do caminho" entre o menor e o maior valor da amostra ou população.

Exemplo:

{4, 1, 3, 4, 8, 8, 7, 9, 11}

Ponto Médio =(1 + 11)/2 = 6

Ponto médio = 6

Frequência (f)

É o número de repetições de um elemento em uma população ou amostra.

Exemplo:

{4,1,3,4,8,8,8,7,11}

Rol = {1,3,4,4,7,8,8,8,11}

f(1) = 1 / f(3) = 1 / f(4) = 2 / f(7) = 1 / f(8) = 3 / f(11) = 1

Separatrizes (Quartil, Percentil, Decil, Quintil)

Quartil (Q)

É a divisão de uma amostra ou população ordenada (Rol) em 4 partes iguais, ou seja, um quarto.

Q₁ = Primeiro Quartil ou Quartil Inferior, é o valor que corresponde a 25% da amostra ordenada ou 25% dos menores valores

Q₂ = Segundo Quartil ou Mediana, é o valor que corresponde a 50% da amostra ordenada

Q₃ = Terceiro Quartil ou Quartil Suoerior, é o valor que corresponde a 75% da amostra ordenada ou 25% dos maiores valores

Construção do Gráfico Box-Plot

Exemplo:

* Quantidade impar de elementos no conjunto

{4, 1, 3, 8, 8, 8, 7, 9, 11}

Rol: {1, 3, 4, 7, 8, 8, 8, 9, 11}

Extremo Inferior = 1

Q_{1 =} {1, 3, 4, 7}  = (3 + 4)/2 = 3,5

Q₂ = {8} = 8 (Mediana)

Q₃ = {8, 8, 9, 11} = (8 + 9) = 8,5

Extremo Superior = 11

Exemplo:

* Quantidade par de elementos no conjunto

{4, 1, 3, 8, 8, 8, 7, 9}

Rol: {1, 3, 4, 7, 8, 8, 8, 9}

Extremo Inferior = 1

Q₁ = {1, 3, 4}  = 3

Q₂ = {7,8} = (7 + 8)/2 = 7,5 (Mediana)

Q₃ = {8, 8, 9} = 8

Extremo Superior = 9

Percentil (P)

É a divisão de uma amostra ou população ordenada (Rol) em 100 partes iguais, ou seja, 99 percentis (99% de dados inferiores).

P₁ a P₉₉  = Primeiro Percentil até o nonoagésimo nono Percentil

P₂₅ = Q₁

P₅₀ = Q₂ (Mediana)

P₇₅ = Q₃

Obs.: Os três principais Percetis (25, 50 e 75) são aqueles que correspondem aos Quartis (1, 2, 3).

Decil (D)

É a divisão de uma amostra ou população ordenada (Rol) em 10 partes iguais, ou seja, a décima parte.

D₅ = P₅₀ = Q₂ (Mediana)

Quintil (K)

É a divisão de uma amostra ou população ordenada (Rol) em 5 partes iguais, ou seja, a quinta parte.

Um grande abraço a todos,

Carlos Roberto Roa