Desafios & Mistérios da Matemática (Fatoração)

Por: Carlos R.
22 de Abril de 2014

Desafios & Mistérios da Matemática (Fatoração)

Matemática EM Equações Produtos Notáveis Fatoração Reais Propriedades Pré-Vestibular Avançado Limítes

Home / Blog profes / Matemática / Carlos R. / Desafios & Mistérios da Matemática (Fatoração)

Encontre um professor e combine aulas particulares Presenciais ou Online

Buscar professor particular

Bom Dia, Turma!

A fatoração nada mais é do que transformar uma equação matemática em uma multiplicação (produto) de fatores. Muitos autores dizem que a fatoração é a simplificação de equações - cuidado!! Isto não é verdade, pois nem sempre uma equação fatorada se torna simplificada!

A fatoração tem como intenção tornar uma equação mais simplificada. Um bom exemplo para nos certificarmos disso é a fatoração da seguinte equação:

$256y^8 - z^8$

Forma fatorada:

$(2y - z)(2y + z)(4y^2 + z^2)(16y^4 + z^4)$

Como podemos perceber, a forma fatorada é bem mais complexa. Veja que existe um conceito bem interessante neste exemplo, está bem evidente que a fatoração busca diminuir o grau do polinômio em seus fatores.

A fatoração, na prática, é utilizada para tornar modelos matemáticos mais complexos em fatores mais simples, por exemplo, a famosa fórmula dos Gases Ideais é (PV = nRT), já a dos Gases Reais é mais refinada e com coeficientes de ajustes referentes ao tipo de gás (a e b).

Fórmula de um Gás Ideal:

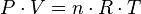
$P \cdot V = n \cdot R \cdot T \,\!$

Fórmula de um Gás Real:

$(P+\frac{a\cdot n^2} { V^2}) \cdot (V-nb) = n \cdot R \cdot T \,\!$

Como podemos perceber, o modelo de um Gás Real é um produto de fatores, com a intenção de simplicar o modelo.

A fatoração, para os mais experientes, é um universo cheio de truques e macetes, é como uma batalha, quanto maior a experiência e o conhecimento das táticas de guerra, mais fácil e rápido será para se atingir o objetivo.

Dica 1 (Utilizando o Triângulo de Pascal)

Uma dica bem interessante é o triângulo de Pascal, na verdade esse triângulo carrega uma série de mistérios bem interessantes, mas vamos, neste artigo, manter o foco na fatoração.

Propriedades do Triângulo de Pascal:

1ª - Um cateto e a hipotenusa do triângulo são formados por 1;
2ª - Em cada linha, os termos equidistantes (mesma distância) dos extremos são iguais;
3ª - O resultado da soma de dois elementos consecutivos de uma linha é imediatamente igual ao elemento da linha abaixo.

$\begin{matrix} &\mathbf{0}&\mathbf{1}&\mathbf{2}&\mathbf{3}&\mathbf{4}&\mathbf{5}&\mathbf{6}&\mathbf{2^{n}}\\ \mathbf{0}&1&&&&&&&{2^{0}=1}\\\mathbf{1}&1&1&&&&&&{2^{1}=2}\\ \mathbf{2}&1&2&1&&&&&{2^{2}=4}\\\mathbf{3}&1&3&3&1&&&&{2^{3}=8}\\ \mathbf{4}&1&4&6&4&1&&&{2^{4}=16}\\ \mathbf{5}&1&5&10&10&5&1&&{2^{5}=32}\\ \mathbf{6}&1&6&15&20&15&6&1&{2^{6}=64} \end{matrix}$

(a + b)^2 = a^2 + 2ab + b^2

(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3

(a + b)^4 = a^4 + 4a^3b^2 + 6a^2b^2 + 4ab^3 + b^4

No triângulo de Pascal, são evidenciados os coeficientes das expressões acima quando aplicados os produtos notáveis.

Dica 2 (Tirando as Cartas das Mangas)

Manter nas mangas as expressões mais clássicas e que são campeãs em provas.

$( a + b)^2 = a^2 + 2ab + b^2$

$(a - b)^2 = a^2 - 2ab + b^2$

$(a + b)(a - b) = a^2 - b^2$

$(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$

$(a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3$

$(a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2ac + 2bc$ (Uma das fatorações mais exploradas em vestibulares militares)

Obs.: As 3 primeiras são primordiais para qualquer prova, a 4ª e a 5ª são desejáveis, já a última é bem específica.

Dica 3 (Aplicando a regra do "Põe e Tira")

Existem questões de fatoração bem inteligentes e que exploram o melhor de nosso raciocínio, são as famosas questões que exigem o "põe e tira", geralmente elas surgem devido a necessidade de formar uma "expressão clássica", supracitada na Dica 2 .

Por exemplo:

1 + 1 = 2, podemos expressar esta sentença da seguinte forma também: 1 + 1 + 7 - 7 = 2, ou seja, o fato de inserirmos o 7 e tirá-lo não afetará o resultado da expressão.

Com esse artifício poderemos resolver o seguinte exercício:

$a^4 + a^2b^2 + b^4$

Resolução:

$a^4 + a^2b^2$ $+ a^2b^2 - a^2b^2$ $+ b^4$

$a^2 + 2a^2b^2 + b^4 - a^2b^2$

$(a^2 + b^2)^2 - a^2b^2$

$(a^2 + b^2) - (ab)^2$

$(a^2 + b^2 - ab)(a^2 + b^2 + ab)$

Dica 4 (Resolvendo como uma Equação Polinomial)

Em uma grande parte dos problemas de fatoração, basta resolvermos a equação igualando-a a zero e encontrando as raízes, pois estas comporão os fatores.

Com essa ideia, poderemos resolver o seguinte exercício:

$a^2 + 6a - 7$

Resolução:

$a^2 + 6a - 7 = 0$ (*)

Igualando a equação do segundo grau a zero temos como raízes, a1 = -7 e a2 = 1.

Sendo assim, a forma fatorada será:

$(a + 7)(a - 1)$

(*)Obs.: Lembre-se que não é correto expor ao examinador a equação sendo igualada a zero, pois é um exercício de fatoração e não de equação do 1º ou do 2º grau.

Dica 5 (Entendendo as Necessidades do Problema)

A dica 5 é somente para os campeões que enxergam a Matrix!!!!!!(hahha...).

Existem questões de Olimpíadas e Vestibulares com um alto grau de dificuldade, em que não basta você conhecer as 4 dicas acima, você terá que extrapolar os limites e "sacar" as necessidades do exercício no decorrer do desenvolvimento. Lembra quando falei da experiência em batalha? Agora você terá que usa-lá! Irei ilustrar este último tópico com um exercício desafiador.

Se $(a + b + c) = 1$ e $(a^2 + b^2 + c^2) = 0$ , calcule $A = a^4 + b^4 + c^4$

Resolução:

$(a + b + c)^2$

Considerando $(b + c) = x$ , para efeito de cálculo teremos:

$(a + x)^2 = (a^2 + 2ax + x^2)$

$(a + b + c)^2 = a^2 + 2a(b + c) + (b + c)^2$

$(a + b + c)^2 = a^2 + 2ab + 2ac + b^2 + 2bc + c^2$

$2ab + 2ab + 2bc = (a + b + c)^2 - (a^2 + b^2 + c^2)$

$2(ab + ac + bc) = (a + b + c)^2 - (a^2 + b^2 + c^2)$

$(ab + ac + bc) = ((a + b + c)^2 - (a^2 + b^2 + c^2))/2$

$(ab + ac + bc) = ((1)^2 - (0))/2$

$(ab + ac + bc) = 1/2$ (Equação I)

$(a^2 + b^2 + c^2)^2$

Considerando $(b^2 + c^2) = y$ , para efeito de cálculo teremos:

$(a^2 + y)^2 = (a^4 + 2a^2y + y^2)$

$(a^2 + b^2 + c^2)^2 = a^4 + 2a^2(b^2 + c^2) + (b^2 + c^2)^2$

$(a^2 + b^2 + c^2)^2 = a^4 + 2a^2b^2 + 2a^2c^2 + b^4 + 2b^2c^2 + c^4$

$(a^4 + b^4 + c^4) = (a^2 + b^2 + c^2)^2 - 2(a^2b^2 + a^2c^2 + b^2c^2)$ (Equação II)

$(ab + ac + bc)^2$

Considerando $(ac + bc) = w$ , para efeito de cálculo temos:

$(ab + w)^2 = (a^2 + 2abw + w^2)$

$(ab + ac + bc)^2 = a^2b^2 + 2ab(ac + bc) + (ac + bc)^2$

$(ab + ac + bc)^2 = a^2b^2 + 2a^2bc + 2ab^2c + a^2c^2 + 2abc^2 + b^2c^2$

$a^2b^2 + a^2c^2 + b^2c^2 = 2a^2bc + 2ab^2c + 2abc^2 - (ab + ac + bc)^2$

$a^2b^2 + a^2c^2 + b^2c^2 = 2abc(a + b + c) - (ab + ac + bc)^2$ (Equação III)

Substituindo a (Equação I em III) e levando-se em consideração que para abc, obrigatoriamente, uma das incógnitas deve ser zero para atender a seguinte equação: $a^2 + b^2 + c^2 = 0$ . A seguir temos:

$a^2b^2 + a^2c^2 + b^2c^2 = 2(0)(1) - (1/2)^2$

$a^2b^2 + a^2c^2 + b^2c^2 = -1/4$ (Equação IV)

Substituindo a (Equação IV em II), temos:

$a^4 + b^4 + c^4 = (0)^2 - 2(-1/4)$

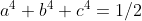$a^4 + b^4 + c^4 = 1/2$ ∴ A = 1/2

Dica Extra (Chamando duas "letras" de uma)

Na resolução do problema acima, existe uma técnica muito utilizada pelos matemáticos para evitar erros e, ao mesmo tempo, organizar o raciocínio, é chamar duas incógnitas de uma "letra", por exemplo, $(a + b) = x$ . Você percebeu que o último item da Dica 2 não precisa necessariamente ser memorizado?

Um grande abraço a todos,

Carlos Roberto Roa

R$ 70 / h

São Paulo / SP

Carlos R.

5,0 (1 avaliação)

12 horas de aula

Matemática para Ensino Fundamental Matemática para Enem Matemática para Ensino Médio

MBA: Data Science - Big Data Analytics (FIA-USP)

Graduado em engenharia e pós-graduado em big data, atuo com inteligência de mercado, buscando ajudar pessoas. Sou criador do site acadêmicos do excel.

Contatar Ver WhatsApp

0 comentários

14 seguidores Seguir blog

Cadastre-se ou faça o login para comentar nessa publicação.

Por: Carlos R.
22 de Abril de 2014

Desafios & Mistérios da Matemática (Fatoração)

Encontre um professor e combine aulas particulares Presenciais ou Online

Dica 1 (Utilizando o Triângulo de Pascal)

Dica 2 (Tirando as Cartas das Mangas)

Dica 3 (Aplicando a regra do "Põe e Tira")

Dica 4 (Resolvendo como uma Equação Polinomial)

Dica 5 (Entendendo as Necessidades do Problema)

$a^4 + b^4 + c^4 = 1/2$ ∴ A = 1/2

Dica Extra (Chamando duas "letras" de uma)

Recursos Profes

O Profes é uma solução completa de aprendizagem, com diversos recursos para
você aprender do jeito mais eficiente e personalizado possível.

Confira artigos similares

Aprenda a utilizar a fórmula ÍNDICE & CORRESP

Aprenda a utiliza a função ÁREAS

Aprenda a utilizar a função SUBTOTAL

Confira mais artigos sobre educação

Exatas

Humanas

Idiomas

Biológicas

Informática

Programação

Música

Comportamento

Encontre um professor particular

Busque, encontre e converse gratuitamente com professores particulares de todo o Brasil

Por: Carlos R. 22 de Abril de 2014

Desafios & Mistérios da Matemática (Fatoração)

Encontre um professor e combine aulas particulares Presenciais ou Online

Dica 1 (Utilizando o Triângulo de Pascal)

Dica 2 (Tirando as Cartas das Mangas)

Dica 3 (Aplicando a regra do "Põe e Tira")

Dica 4 (Resolvendo como uma Equação Polinomial)

Dica 5 (Entendendo as Necessidades do Problema)

∴ A = 1/2

Dica Extra (Chamando duas "letras" de uma)

Recursos Profes

O Profes é uma solução completa de aprendizagem, com diversos recursos para você aprender do jeito mais eficiente e personalizado possível.

Confira artigos similares

Aprenda a utilizar a fórmula ÍNDICE & CORRESP

Aprenda a utiliza a função ÁREAS

Aprenda a utilizar a função SUBTOTAL

Confira mais artigos sobre educação

Exatas

Humanas

Idiomas

Biológicas

Informática

Programação

Música

Comportamento

Encontre um professor particular

Busque, encontre e converse gratuitamente com professores particulares de todo o Brasil

Por: Carlos R.
22 de Abril de 2014

$a^4 + b^4 + c^4 = 1/2$ ∴ A = 1/2

O Profes é uma solução completa de aprendizagem, com diversos recursos para
você aprender do jeito mais eficiente e personalizado possível.