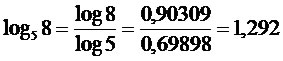Propriedades da Função Logaritmo

Propriedades para auxiliar na operação de um Logaritmo

Os logaritmos possuem inúmeras aplicações no cotidiano, a Física e a Química utilizam as funções logarítmicas nos fenômenos em que os números adquirem valores muito grandes, tornando-os menores, facilitando os cálculos e a construção de gráficos. O manuseio dos logaritmos requer algumas propriedades que são fundamentais para o seu desenvolvimento. Veja:

Propriedade do produto do logaritmo

Se encontrarmos um logaritmo do tipo: log_a(x * y) devemos resolvê-lo, somando o logaritmo de x na base a e o logaritmo de y na base a.

log_a (x * y) = log_a x + log_a y

Exemplo:
log₂(32 * 16) = log₂32 + log₂16 = 5 + 4 = 9


Propriedades do quociente do logaritmo

Caso o logaritmo seja do tipo log_ax/y, devemos resolvê-lo subtraindo o logaritmo do numerador na base a pelo logaritmo do denominador também na base a.

log_ax/y = log_ax – log_ay

Exemplo:
log₅(625/125) = log₅625 – log₅125 = 4 – 3 = 1


Propriedade da potência do logaritmo

Quando um logaritmo estiver elevado a um expoente, na próxima passagem esse expoente irá multiplicar o resultado desse logaritmo, veja como:

log_ax^m = m*log_ax

Exemplo:
log₃81² = 2*log₃81 = 2 * 4 = 8



Propriedade da raiz de um logaritmo

Essa propriedade é baseada em outra, que é estudada na propriedade da radiciação, ela diz o seguinte:



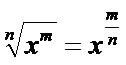
Essa propriedade é aplicada no logaritmo quando:

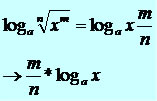
Exemplo:

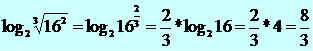
Propriedade da mudança de base

Existem situações nas quais precisaremos utilizar a tábua de logaritmos ou uma calculadora científica na determinação do logaritmo de um número. Mas para isso devemos trabalhar o problema no intuito de estabelecer o logaritmo na base 10, pois as tábuas e as calculadoras operam nessas condições, para isso utilizamos a propriedade da mudança de base, que consiste na seguinte definição:

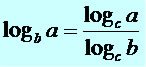
Exemplo