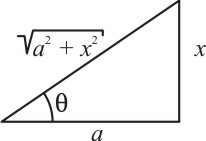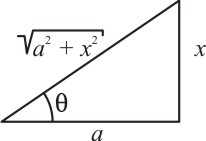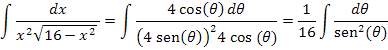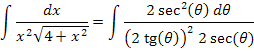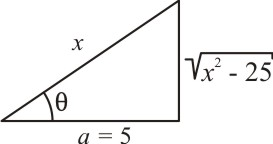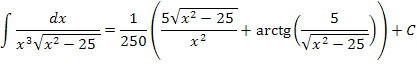Integração por Substituição Trigonométrica

Há meios diferentes para integrar uma função e para cada integral, devemos identificar qual o melhor dos métodos a aplicar. Somente resolvendo diversos exemplos para podermos nos familiarizar com cada um desses métodos.

No caso de integração por substituição trigonométrica, um integrante que contenha uma das formas:

sendo a uma constante positiva e não tendo nenhum outro fator irracional, pode ser transformado numa integral trigonométrica mais familiar, utilizando substituições trigonométricas ou com o emprego de uma nova variável.

Para os três casos acima, utilizamos as identidades trigonométricas:

Vamos ver cada um desses casos separadamente.

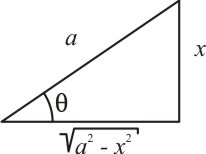
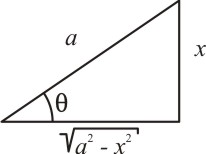
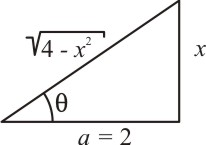
Caso I: Para uma integral que envolva um radical do tipo , fazemos a mudança de variável de x para θ. A substituição deve ser apropriada e fica melhor observada no triângulo retângulo:

Temos que:

Assim,  substitui  por , pois:

E pela identidade trigonométrica dada em (1), obtemos:

Extraindo a raiz de ambos os membros da equação acima, obtemos:

Justificando a substituição.

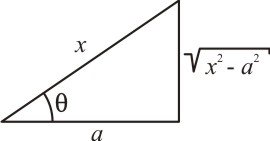
Caso II: Para uma integral que envolva um radical do tipo , fazemos a mudança de variável de x para θ. Observando o triângulo retângulo:

Temos que:

Assim,  substitui  por , pois:

E pela identidade trigonométrica dada em (2), obtemos:

Extraindo a raiz de ambos os membros da equação acima, obtemos:

Justificando a substituição.

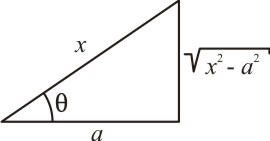
Caso III: Para uma integral que envolva um radical do tipo , fazemos a mudança de variável de x para θ. Observando o triângulo retângulo:

Temos que:

Assim,  substitui  por , pois:

E pela identidade trigonométrica dada em (3), obtemos:

Extraindo a raiz de ambos os membros da equação acima, obtemos:

Justificando a substituição.

Com base nos resultados obtidos, podemos montar uma tabela:

Vejam que, para representar graficamente as substituições sugeridas no triângulo retângulo, o radical ficará sempre no lado do triângulo que não é utilizado pela relação trigonométrica:

Caso I: Usa-se x = a sen(θ); logo, o radical aparece no cateto adjacente a θ.

Caso II: Usa-se x = a tg(θ); logo, o radical aparece na hipotenusa.

Caso III: Usa-se a sec(θ); logo, o radical aparece no cateto oposto a θ.

Vejamos alguns exemplos para ilustrar o método.

Exemplo 1: Calcule a integral abaixo:

Esta é uma integral do tipo I. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:

Assim:

Devemos agora, reescrever o resultado em termos da variável original x. Observando o triângulo retângulo, devemos encontrar as relações trigonométricas que aparecem no resultado acima. Assim:

Assim:

Exemplo 2: Calcule a integral abaixo:

Esta é uma integral do tipo II. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:

Assim:

Vamos, agora, reescrever o resultado em termos da variável original x. Observando o triângulo, encontramos as relações:

Assim:

Como C é uma constante arbitrária e ln(a) também é uma constante, podemos reescrever o resultado como:

Exemplo 3: Calcule a integral abaixo:

Esta é uma integral do tipo III. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:

Assim:

Vamos reescrever o resultado em termos da variável original x. Observando o triângulo encontramos as relações:

Assim:

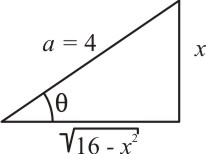
Exemplo 4: Calcule a integral abaixo:

Esta é uma integral do tipo I. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:

Assim:

Agora, reescrevemos o resultado em termos da variável original x. Observando o triângulo retângulo, encontramos a relação:

Assim:

Exemplo 5: Calcule a integral abaixo:

Esta é uma integral do tipo II. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:

Assim:

Reescrevendo o resultado em termos da variável x e utilizando as relações observadas no triângulo retângulo, fazemos:

Assim:

Exemplo 6: Calcule a integral abaixo:

Esta é uma integral do tipo III. Vamos fazer a representação no triângulo retângulo:

Assim, escrevemos:

Assim:

Vejam aqui como integrar cos2(θ).

Agora, representamos o resultado em termos da variável original x. Observando o triângulo retângulo, encontramos as relações:

Assim:

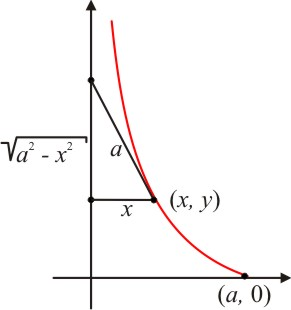
Exemplo 7: Para ilustrar o uso desse método, vamos determinar a equação datractriz, que é uma curva definida pela trajetória de um objeto arrastado ao longo de um plano horizontal por um fio de comprimento constante quando a outra extremidade do fio se move ao longo de uma reta no plano. A palavratractriz provém do latim tractum, que significa draga.

Vamos considerar um plano formado por eixos ortogonais xy e o objeto comece no ponto (a, 0) com a outra extremidade do fio na origem. Se esta se move para cima ao longo do eixo dos y:

o fio será sempre tangente à curva e o comprimento da tangente entre o eixo dosy e o ponto de contato será sempre igual a a. O coeficiente angular da tangente é dado pela fórmula:

Separando as variáveis e usando o resultado do exemplo 1, temos:

Quando x = a, y = 0 e C = 0. Logo:

que é a equação da tractriz.

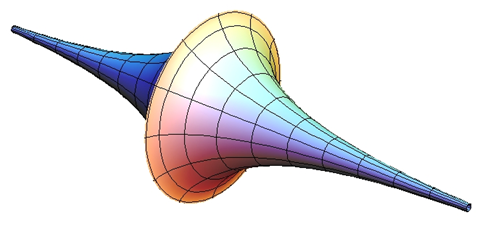
Se as extremidades do fio movem-se para baixo no eixo dos y, então uma outra parte da curva é gerada. Se girarmos essas duas partes em torno do eixo dos y, a superfície resultante será uma pseudo-esfera, com forma de uma “corneta dupla”.

Exercícios para Casa:

Referência Bibliográfica

O BARICENTRO DA MENTE. Integração por substituição trigonométrica. Disponível em: <http://obaricentrodamente.blogspot.com.br/2012/06/integracao-por-substituicao.html> Acessado em: 24 de junho de 2015.