Determinantes

Matemática Ensino Médio Álgebra Geral Teoria dos Números

O determinante é um número associado a uma matriz quadrada. Esse número é encontrado fazendo-se determinadas operações com os elementos que compõe a matriz.

Indicamos o determinante de uma matriz A por det A. Podemos ainda, representar o determinante por duas barras entre os elementos da matriz.

Determinantes de 1.ª Ordem

O determinante de uma matriz de Ordem 1, é igual ao próprio elemento da matriz, pois esta apresenta apenas uma linha e uma coluna.

Exemplos:

$det espaço reto X espaço igual a espaço linha vertical 8 linha vertical espaço igual a espaço 8 espaço det espaço reto Y espaço igual a espaço linha vertical menos 5 linha vertical espaço igual a espaço 5$

Determinantes de 2.ª Ordem

As matrizes de Ordem 2 ou matriz 2x2, são aquelas que apresentam duas linhas e duas colunas.

O determinante de uma matriz desse tipo é calculado, primeiro multiplicando os valores constantes nas diagonais, uma principal e outra secundária.

A seguir, subtraindo os resultados obtidos dessa multiplicação.

Exemplos:

Matriz A =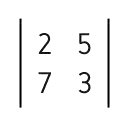 Exemplo de Determinante de 2.º Ordem

$d e t espaço A espaço igual a espaço 3 espaço sinal de multiplicação espaço 2 espaço menos espaço 7 espaço sinal de multiplicação espaço 5 d e t espaço A espaço igual a espaço 6 espaço menos espaço 35 espaço d e t espaço A espaço igual a menos 29$

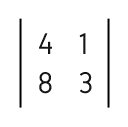
Matriz B = Exemplo de Determinantes de 2.ª Ordem

$d e t espaço B espaço igual a espaço 3 espaço sinal de multiplicação espaço 4 espaço menos espaço 8 espaço sinal de multiplicação espaço 1 espaço d e t espaço B espaço igual a 12 espaço menos espaço 8 d e t espaço B espaço igual a espaço 4$

Determinantes de 3.ª Ordem

As matrizes de Ordem 3 ou matriz 3x3, são aquelas que apresentam três linhas e três colunas:

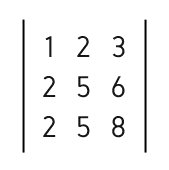
Exemplo de Determinantes de 3.ª Ordem

Para calcular o determinante desse tipo de matriz, utilizamos a Regra de Sarrus, que consiste em repetir as duas primeiras colunas logo a seguir à terceira:

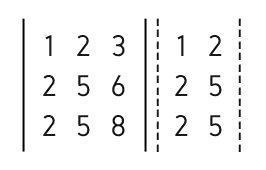
Exemplo de Determinantes de 3.ª Ordem

Seguimos os seguintes passos:

1) Calculamos a multiplicação em diagonal. Para tanto, traçamos setas diagonais que facilitam o cálculo.

As primeiras setas são traçadas da esquerda para a direita e correspondem às diagonais principais:

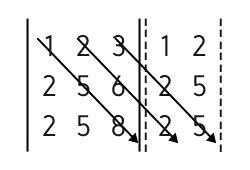
Exemplo de Determinantes de 3.ª Ordem

$1 espaço sinal de multiplicação espaço 5 espaço sinal de multiplicação espaço 8 espaço igual a espaço 40 espaço 2 espaço sinal de multiplicação espaço 6 espaço sinal de multiplicação espaço 2 espaço igual a espaço 24 espaço 3 espaço sinal de multiplicação espaço 2 espaço sinal de multiplicação espaço 5 espaço igual a espaço 30$

2) Calculamos a multiplicação do outro lado da diagonal. Assim, traçamos novas setas.

Agora, as setas são traçadas da direita para a esquerda e correspondem à diagonal secundária:

Matriz A =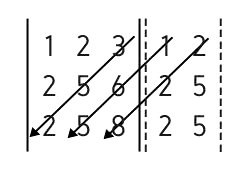 Exemplo de Determinantes de 3.ª Ordem

$2 espaço sinal de multiplicação espaço 2 espaço sinal de multiplicação espaço 8 espaço igual a espaço 32 espaço 1 espaço sinal de multiplicação espaço 6 espaço sinal de multiplicação espaço 5 espaço igual a espaço 30 espaço 3 espaço sinal de multiplicação espaço 5 espaço sinal de multiplicação espaço 2 espaço igual a espaço 30$

3) Somamos cada uma delas:

$P r o d u t o espaço d a s espaço d i a g o n a i s espaço p r i n c i p a i s 40 espaço mais espaço 24 espaço mais espaço 30 espaço igual a espaço 94 espaço P r o d u t o espaço d a s espaço d i a g o n a i s espaço s e c u n d á r i a s 32 espaço mais espaço 30 espaço mais espaço 30 espaço igual a espaço 92$

4) Subtraímos cada um desses resultados:

$94 espaço menos espaço 92 espaço igual a espaço 2$

Logo, o determinante é:
$det espaço reto A espaço igual a espaço 2$