Diagonais de um polígono

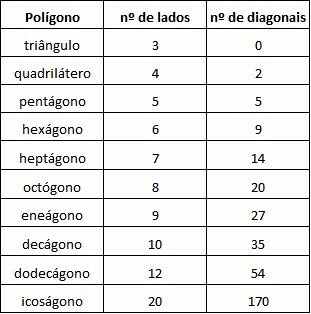
As diagonais em um polígono são segmentos de reta que ligam dois vértices não consecutivos através de sua região interna.

Assim, para traçar uma diagonal, é preciso começar em um vértice e seguir com o traço até outro, que não seja vizinho, uma vez que o segmento deve cortar o interior do polígono. Perceba que se o traço seguir para um vértice consecutivo, ele se torna o próprio lado.

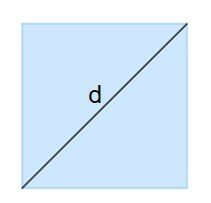
É importante lembrar que um polígono é uma figura fechada plana, formada por segmentos de reta consecutivos que se ligam nos vértices, o encontro entre os lados. São estes segmentos que formam os lados que, dependendo da quantidade, darão o nome do polígono, como: triângulos, quadriláteros, pentágonos, etc.

Número de diagonais em um polígono

Como uma diagonal é um segmento que liga dois vértices, quanto maior o número de vértices, maior será o número de diagonais.

Em um polígono o número de vértices é igual ao número de lados. Assim, um quadrado possui quatro lados e quatro vértices.

Não é todo tipo de polígono que é possível conhecer a quantidade de diagonais, apenas os convexos. Estes polígonos, os convexos, não possuem concavidade, são aqueles que seus ângulos internos são menores que 180º.

Fórmula do número de diagonais: calculando a quantidade em polígonos convexos

O número de diagonais em um polígono convexo é calculado pela fórmula:

Onde,
d é o número de diagonais,
n é o número de lados (que é igual ao número de vértices).

Repare que (n - 3) é o número de diagonais que partem de um único vértice. Em um quadrado, por exemplo, apenas uma diagonal parte de cada vértice, pois 4 - 3 = 1.

É fácil perceber que um triângulo não há diagonais, visto que n - 3 = 0. Já em um quadrilátero, basta traçarmos um “x” para verificar que possuem duas diagonais.

Esta quantidade é multiplicada pelo número lados, ou número de vértices, representado pelo letra n. Como isso faz com que uma diagonal seja contada duas vezes, temos que dividir o resultado por dois. Assim, chegamos a fórmula.

Quantas diagonais tem um pentágono

Pentágono é o polígono com cinco lados, logo, cinco vértices. Utilizando a fórmula, temos:

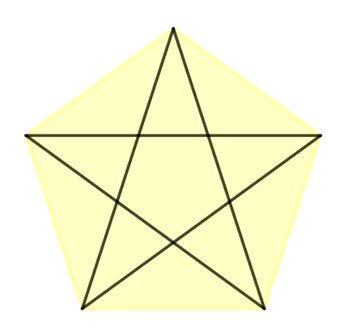
Tabela de polígonos e suas diagonais