Resolva a lista de exercícios sobre fórmula de Bhaskara e tire suas dúvidas com exercícios resolvidos e comentados.
Fórmula de Bhaskara
Onde: 
a é o coeficiente junto ao 
,
b é o coeficiente junto ao 
,
c é o coeficiente independente.
Exercício 1
Utilizando a fórmula de Bhaskara, determine as raízes da equação 
.
Determinando o delta
Determinando as raízes da equação
Exercício 2
O conjunto solução que torna a equação 
verdadeira é
a) S={1,7}
b) S={3,4}
c) S={2, -7}.
d) S={4,5}
e) S={8,3}
Resposta correta: c) S={2, -7}.
Os coeficientes são:
a = 1
b = 5
c = -14
Determinando o delta
Utilizando a fórmula de Bhaskara
O conjunto solução da equação é S={2, -7}.
Exercício 3
Determine os valores de x que satisfaçam a equação 
.
Utilizando a propriedade distributiva da multiplicação, temos:
Os termos da equação do segundo grau são:
a = -1
b = 1
c = 12
Calculando o delta
Utilizando a fórmula de Bhaskara para determinar as raízes da equação:
Os valores de x que satisfazem a equação são x = -3 e x = 4.
Exercício 4
Sendo a seguinte equação do segundo grau, 
, determine o produto entre as raízes.
Resposta correta: -8/3
Determinando as raízes da equação através da fórmula de Bhaskara.
Os coeficientes são:
a = 3
b = 2
c = -8
Delta
Cálculo das raízes
Determinando o produto entre as raízes.
Exercício 5
Classifique as equações que possuem raízes reais.
Respostas corretas: II, III e IV.
Não há raízes reais em equações com 
negativo pois, na fórmula de Bhaskara ele é o radicando de uma raiz quadrada e, não existe raiz quadrada de números negativos nos números reais.
Delta negativo, portanto I não possui solução real.
Delta positivo, portanto II possui solução real.
Delta negativo, portanto III não possui resolução real.
Delta positivo, portanto IV possui solução real.
Exercício 6
O seguinte gráfico é determinado pela função do segundo grau 
. O parâmetro c, indica o ponto de intersecção da curva com o eixo y. As raízes x1 e x2 são os números reais que, quando substituídos na equação a tornam verdadeira, ou seja, os dois lados da igualdade serão iguais a zero. Com base nas informações e no gráfico, determine o parâmetro c.
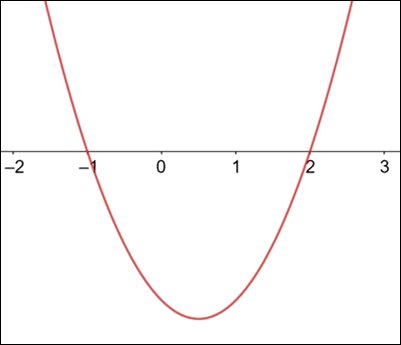
Resposta correta: c = -2.
Objetivo
Determinar c.
Resolução
As raízes são os pontos em que a curva corta o eixo x, das abcissas. Desta forma, as raízes são:
Os parâmetros são:
A fórmula de Bhaskara é uma igualdade que relaciona todos estes parâmetros.
Para determinar o valor de c, basta isolá-lo na fórmula e, para isto, vamos arbitrar uma das raízes, utilizando a de maior valor, por consequência o valor positivo do delta.
Neste ponto, elevamos os dois lados da equação ao quadrado para retirar a raiz do delta.
Substituindo os valores numéricos:
Desta forma, o parâmetro c é -2.
Exercício 7
(Prefeitura de São José dos Pinhais - PR 2021) Assinale a alternativa que traga uma afirmação correta da maior das soluções da equação:
a) É ímpar.
b) É negativo.
c) É múltiplo de 4.
d) É um quadrado perfeito.
e) É igual a zero.
Resposta correta: a) É ímpar.
Parâmetros da equação:
a = 1
b = 2
c = -15
Sendo a maior solução da equação, 3, é um número ímpar.
Exercício 8
(PUC - 2016)
Considere um triângulo retângulo de hipotenusa a e catetos b e c, com b > c, cujos lados obedeçam a essa regra. Se a + b + c = 90, o valor de a . c, é
a) 327
b) 345
c) 369
d) 381
Resposta correta: c) 369.
Os termos entre parênteses equivalem aos lados a, b e c do triângulo retângulo.
O enunciado também fornece que a + b + c = 90, dessa forma, substitui-se os termos da tríade pitagórica. Se tratando de uma soma, a ordem não importa.
Resolvendo a equação do segundo grau para determinar m:
Os coeficientes são,
a = 1
b = 1
c = -90
Como se trata de uma medida, desconsideraremos m2, pois não existe medida negativa.
Substituindo o valor 9 nos termos:
Em um triângulo retângulo, a hipotenusa é o maior lado, logo a = 41. O menor lado é o c, de acordo com o enunciado, logo, c = 9.
Desta forma, o produto é:
Exercício 9
Fórmula de Bhaskara e planilha eletrônica
(CRF-SP - 2018) A fórmula de Bhaskara é um método para encontrar as raízes reais de uma equação do segundo grau fazendo uso apenas de seus coeficientes. Vale lembrar que coeficiente é o número que multiplica uma incógnita em uma equação. Em sua forma original, a fórmula de Bhaskara é dada pela seguinte expressão:
Discriminante é a expressão presente dentro da raiz na fórmula de Bhaskara. É comumente representado pela letra grega Δ (Delta) e recebe esse nome pelo fato de discriminar os resultados de uma equação da seguinte maneira: Assinale a alternativa que transcreve corretamente a fórmula Δ = b2 – 4.a.c na célula E2.
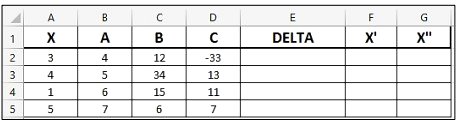
a) =C2*(C2-4)*B2*D2.
b) =(B2^B2)-4*A2*C2.
c) =POTÊNCIA(C2;2)-4*B2*D2.
d) =POTÊNCIA(C2;C2)-4*B2*D2.
Resposta correta: c) =POTÊNCIA(C2;2)-4*B2*D2.
A equação do delta deve ser digitada na célula E2 (coluna E e linha 2). Por isto, os parâmetros são todos da linha 2.
Em uma planilha eletrônica toda fórmula começa com o símbolo de igualdade =.
Como a equação do delta começa com 
, na planilha, a fórmula de possuir uma potência, assim, descartamos as opções a) e b).
Na planilha o parâmetro b está na célula C2 e, é o valor que está nesta célula que deve ser elevado ao quadrado.
A construção da função potência em uma planilha eletrônica fica assim:
1) Para chamar a função potência, digita-se: =POTÊNCIA
2) A base e o expoente vem logo em seguida, entre parênteses, separados com ponto e vírgula ;
3) Primeiro a base, depois o expoente.
Desta forma a função fica:
Ver WhatsApp