Introdução às matrizes

Os tipos de matrizes incluem as diversas maneiras de representação de seus elementos. São classificadas em: matriz linha, coluna, nula, quadrada, transposta, oposta, identidade, inversa e iguais.

Definição de Matriz

Antes de mais nada, devemos atentar ao conceito de matriz. Trata-se de uma representação matemática que inclui em linhas (horizontais) e colunas (verticais) alguns números naturais não-nulos.

Os números, chamados de elementos, são representados entre parênteses ou colchetes.

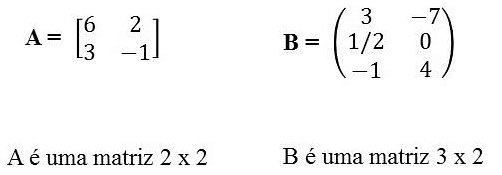
Classificação das Matrizes

Matrizes Especiais

Há quatro tipos de matrizes especiais:

• Matriz Linha: formada por uma única linha, por exemplo:

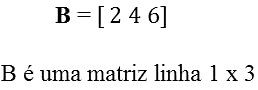
• Matriz Coluna: formada por uma única coluna, por exemplo:

• Matriz Nula: formada por elementos iguais a zero, por exemplo:

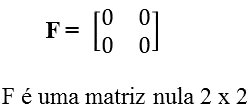
• Matriz Quadrada: formada pelo mesmo número de linhas e colunas, por exemplo:

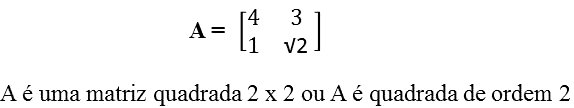
Matriz Transposta

A matriz transposta  (indicada pela letra t) é aquela que apresenta os mesmos elementos de uma linha ou coluna comparada com outra matriz.

No entanto, os elementos iguais entre as duas são invertidos, ou seja, a linha de uma apresenta os mesmos elementos que a coluna de outra. Ou ainda, a coluna de uma possui os mesmos elementos da linha de outra.

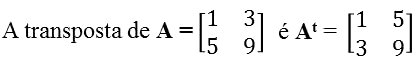
Matriz Oposta

Na matriz oposta, os elementos entre duas matrizes apresentam sinais diferentes, por exemplo:

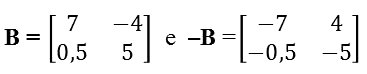
Matriz Identidade

A Matriz .Identidade ocorre quando os elementos da diagonal principal são todos iguais a 1 e os outros elementos são iguais a 0 (zero):

Matriz Inversa

A matriz inversa é uma matriz quadrada. Ela ocorre quando o produto de duas matrizes for igual a uma matriz identidade quadrada de mesma ordem.

A . B = B . A = I_n (quando a matriz B é inversa da matriz A)

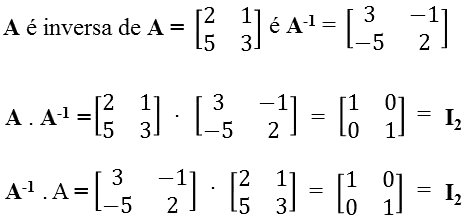
Obs: Para encontrar a matriz inversa utiliza-se a multiplicação de matrizes.

Igualdade de Matrizes

Quando temos matrizes iguais, os elementos das linhas e das colunas são correspondentes:

Exercícios de Vestibular com Gabarito

1. (U.F. Uberlândia-MG) Sejam A, B e C matrizes quadradas de ordem 2, tais que A . B = I, em que I é a matriz identidade.
A matriz X tal qual A . X . A = C é igual a:

a) B . C . B
b) (A²) ^-1 . C
c) C . (A^-1)²
d) A . C . B