Juros simples e compostos

Os juros simples e compostos são cálculos efetuados com o objetivo de corrigir os valores envolvidos nas transações financeiras, isto é, a correção que se faz ao emprestar ou aplicar uma determinada quantia durante um período de tempo.

O valor pago ou resgatado dependerá da taxa cobrada pela operação e do período que o dinheiro ficará emprestado ou aplicado. Quanto maior a taxa e o tempo, maior será este valor.

Diferença entre juros simples e compostos

Nos juros simples a correção é aplicada a cada período e considera apenas o valor inicial. Nos juros compostos a correção é feita em cima de valores já corrigidos.

Por isso, os juros compostos também são chamados de juros sobre juros, ou seja, o valor é corrigido sobre um valor que já foi corrigido.

Sendo assim, para períodos maiores de aplicação ou empréstimo a correção por juros compostos fará com que o valor final a ser recebido ou pago seja maior que o valor obtido com juros simples.

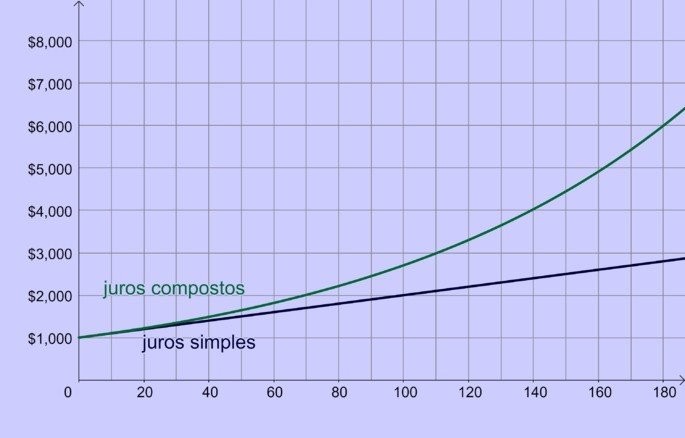
A maioria das operações financeiras utiliza a correção pelo sistema de juros compostos. Os juros simples se restringem as operações de curto período.

Fórmula de juros simples

Os juros simples são calculados aplicando a seguinte fórmula:

Sendo,

J: juros
C: valor inicial da transação, chamado em matemática financeira de capital
i: taxa de juros (valor normalmente expresso em porcentagem)
t: período da transação

Podemos ainda calcular o valor total que será resgatado (no caso de uma aplicação) ou o valor a ser quitado (no caso de um empréstimo) ao final de um período predeterminado.

Esse valor, chamado de montante, é igual a soma do capital com os juros, ou seja:

Podemos substituir o valor de J, na fórmula acima e encontrar a seguinte expressão para o montante:

A fórmula que encontramos é uma função afim, desta forma, o valor do montante cresce linearmente em função do tempo.

Exemplo

Se o capital de R$ 1 000,00 rende mensalmente R$ 25,00, qual é a taxa anual de juros no sistema de juros simples?

Solução

Primeiro, vamos identificar cada grandeza indicada no problema.

C = R$ 1 000,00
J = R$ 25,00
t = 1 mês
i = ?

Agora que fizemos a identificação de todas as grandezas, podemos substituir na fórmula dos juros:

Entretanto, observe que essa taxa é mensal, pois usamos o período de 1 mês. Para encontrar a taxa anual precisamos multiplicar esse valor por 12, assim temos:

i = 2,5.12= 30% ao ano

Fórmula de juros compostos

O montante capitalizado a juros compostos é encontrado aplicando a seguinte fórmula:

Sendo,

M: montante
C: capital
i: taxa de juros
t: período de tempo

Diferente dos juros simples, neste tipo de capitalização, a fórmula para o cálculo do montante envolve uma variação exponencial. Daí se explica que o valor final aumente consideravelmente para períodos maiores.

Exemplo

Calcule o montante produzido por R$ 2 000,00 aplicado à taxa de 4% ao trimestre, após um ano, no sistema de juros compostos.

Solução

Identificando as informações dadas, temos:

C = 2 000
i = 4% ou 0,04 ao trimestre
t = 1 ano = 4 trimestres
M = ?

Substituindo esses valores na fórmula de juros compostos, temos:

Observação: o resultado será tão melhor aproximado quanto o número de casas decimais utilizadas na potência.

Portanto, ao final de um ano o montante será igual a R$ 2 339,71.

Exercícios Resolvidos

Questão 1

Cálculo do montante

Qual o montante de uma aplicação de R$500,00, a uma taxa de 3% ao mês, em um período de 1 ano e 6 meses, nos sistemas de juros simples e compostos?

Juros simples

Juros compostos

Questão 2

Cálculo do capital

Um certo capital foi aplicado por um período de 6 meses. A taxa foi de 5% ao mês. Após esse período, o montante era de R$5000,00. Determine o capital.

Juros simples

Colocando C em evidência na fórmula de juros simples:

M = C + J

M = C + C.i.t

M = C(1+i.t)

Isolando C na equação:

Juros compostos