Retas concorrentes

Duas retas distintas que estão em um mesmo plano são concorrentes quando possuem um único ponto em comum.

As retas concorrentes formam entre si 4 ângulos e de acordo com as medidas desses ângulos, elas podem ser perpendiculares ou oblíquas.

Quando os 4 ângulos formados por elas são iguais a 90º, elas são chamadas perpendiculares.

Na figura abaixo as retas r e s são concorrentes perpendiculares.

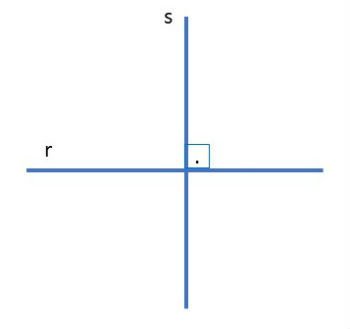
Já se os ângulos formados forem diferentes de 90º, elas são chamadas concorrentes oblíquas. Na figura abaixo representamos as retas u e v oblíquas.

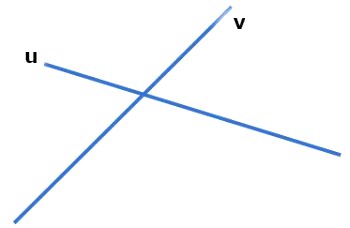
Posição Relativa de Duas Retas

Conhecendo as equações de duas retas podemos verificar suas posições relativas. Para isso devemos resolver o sistema formado pelas equações das duas retas. Assim temos:

• Retas concorrentes: o sistema é possível e determinado (um único ponto em comum).
• Retas coincidentes: o sistema é possível e determinado (infinitos ponto em comum).
• Retas paralelas: o sistema é impossível (nenhum ponto em comum).

Exemplo:

Determine a posição relativa entre a reta r: x - 2y - 5 = 0 e a reta s: 2x - 4y - 2 = 0.

Solução:

Para encontrar a posição relativa entre as retas dadas, devemos calcular o sistema de equações formado por suas retas, assim temos:

Ao resolver o sistema por adição encontramos a seguinte equação 0y = - 8, como não existe solução para essa equação, ele é impossível. Desta forma, as duas retas são paralelas.

Ângulos Opostos pelo Vértice

Duas retas concorrentes formam dois pares de ângulos. Estes ângulos possuem um ponto em comum que é chamado de vértice.

Os pares de ângulos que são opostos pelo vértice são congruentes, ou seja, possuem a mesma medida.

Na figura abaixo, representamos os ângulos AÔB e CÔD que são opostos pelo vértice, assim como os ângulos AÔC e BÔD.

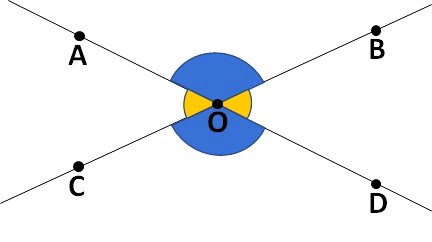
Ponto de Intersecção entre Duas Retas Concorrentes

O ponto de intersecção entre duas retas concorrentes pertence às equações das duas retas. Desta forma, podemos encontrar as coordenadas desse ponto em comum, resolvendo o sistema formado pelas equações dessas retas.

Exemplo:

Determine as coordenadas de um ponto P comum as retas r e s, cujas equações são x + 3y + 4 = 0 e 2x - 5y - 2 = 0, respectivamente.

Solução:

Para encontrar as coordenadas do ponto, devemos resolver o sistema com as equações dadas. Assim temos:

Resolvendo o sistema, temos:

Substituindo esse valor na primeira equação encontramos:

Logo, as coordenadas do ponto de intersecção são, ou seja.

Retas Concorrentes, Coincidentes e Paralelas

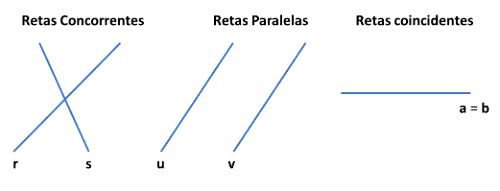
Duas retas que pertençam a um mesmo plano podem ser concorrentes, coincidentes ou paralelas.

Enquanto as retas concorrentes apresentam um único ponto de intersecção, as retas coincidentes possuem pelo menos dois pontos em comum e as retas paralelas não possuem pontos em comum.

Exercícios Resolvidos

1) Em um sistema de eixos ortogonais, - 2x + y + 5 = 0 e 2x + 5y - 11 = 0 são, respectivamente, as equações das retas r e s. Determine as coordenadas do ponto de intersecção de r com s.

2) Quais as coordenadas dos vértices de um triângulo, sabendo que as equações das retas-suporte de seus lados são: - x + 4y - 3 = 0, - 2x + y + 8 = 0 e 3x + 2y - 5 = 0 ?

3) Determine a posição relativa das retas r: 3x - y -10 = 0 e s: 2x + 5y - 1 = 0.