Resolva suas atividades acadêmicas

Envie sua atividade e um professor resolve

Enviar atividade

Tintim por tintim: velocidade terminal de uma bola

Por: Marcus V.
09 de Junho de 2020

Tintim por tintim: velocidade terminal de uma bola

Física Mecânica

Na série de textos tintim por tintim, apresento a resolução bem detalhada de problemas desafiadores.

Retirado do livro 'Física I', de Sears & Zemansky. Capítulo 5, exercício 5.124.

Considere uma bola lançada do alto de um edifício., considerando que o ar durante a queda exerce uma força 'f' sobra a bola. Em queda livre, atua sobre a bola duas forças, seu peso P, para baixo e a força f para cima, na direção contrária ao movimento. Usando a segunda lei de Newton e as expressões para o peso P e a força de arrasto f, temos:

$\sum F = m a$ $f = Dv^2$ $P=mg$ $a = dv/dt$

$m dv/dt = P - f$ -> $m dv/dt = mg - Dv^2$ .

A força de arrasto f, sendo proporcional a velocidade ao quadrado, aumenta ( reduzindo a aceleração da bola ) até que seu valor se iguale ao peso. Neste momento a aceleração é nula e o movimento passa a ser retilíneo uniforme, atingindo a velocidade terminal.

Seja $v_T$ a velocidade terminal. Usando a informação dita anteriormente temos:

$dv_T/dt = 0$ Usando a segunda lei de Newton: $0 = mg - Dv_T^2$ -> $v_T = \sqrt(mg/D)$ velocidade terminal (1)

Como seria a descrição da velocidade em função do tempo, sabendo que a velocidade inicial é nula ? Considere a equação diferencial:

$m \frac{dv}{dt} = mg - Dv^2$ -> $m dv = (mg - Dv^2) dt$ -> $\frac{mdv}{(mg - Dv^2)}=dt$ -> $\frac{mdv}{D(mg/D - v^2)} = dt$ -> $\frac{dv}{(mg/D - v^2)} = \frac{D}{m}dt$

Na expressão anterior, ao lado esquerdo temos a variável de integração v e uma constante mg/D, no denominador.

fazendo substituição de variáveis: $x = v$ $a^2 = mg/D$ a expressão se torna:

$\frac{dx}{(a^2 - x^2)} = \frac{g}{a^2} dt$ (2)

A continuidade da solução exige que seja feito a integração em ambos lados da igualdade. No lado esquerdo usaremos o método das frações parciais:

$\frac{1}{(a^2 - x^2)} =$ $\frac{A}{(a-x)} + \frac{B}{(a+x)}$ $= \frac{A(a+x) + B(a-x)}{(a-x)(a+x)} =$ $\frac{ a(A+B) +x(A-B)}{(a^2 - x^2)}$

a igualdade impõe que:

$x(A-B) = 0$ $A=B$ (3)

$a(A+B) = 1$ usando o resultado anterior: $2aA= 1$ -> $A = 1/2a$ (4)

Usando os resultados (3) e (4) podemos retomando o calculo do lado esquerdo da integral (2) :

$\int \frac{dx}{(a^2 - x^2)} =$ $\frac{1}{2a} \int \Big\[ \frac{1}{(a-x)} + \frac{1}{(a+x)} \Big\] dx =$ $\frac{1}{2a} \Big\[ \int \frac{dx}{(a-x)} + \int \frac{dx}{(a+x)} \Big\] =$

$\frac{1}{2a} \Big\[ -ln(a-x) + ln(a+x) \Big\] =$ $\frac{1}{2a} ln \Big\[ \frac{(a+x)}{(a-x)} \Big\]$ Usando o resultado e integrando o lado direito da igualdade (2):

$\frac{1}{2a} ln \Big\[ \frac{(a+x)}{(a-x)} \Big\] = \frac{gt}{a^2}$ -> $ln \Big\[ \frac{(a+x)}{(a-x)} \Big\] = \frac{2gt}{a}$ -> $\frac{(a+x)}{(a-x)} = exp \Big\[ \frac{2gt}{a} \Big\]$

$(a+x) =(a-x) exp \Big\[ \frac{2gt}{a} \Big\]$ -> $x( exp [2gt/a] + 1) = a(exp [2gt/a] - 1)$ -> $x = a \frac{(exp [2gt/a] - 1)}{( exp [2gt/a] + 1)}$ -> $x =a \frac{( e^{gt/a} + e^{-gt/a})}{( e^{gt/a} - e^{-gt/a})}$

$v = a* tgh\Big\[ \frac{gt}{a} \Big\]$

Análise dimensional: [a²] = [kg][m/s²]/[Kg/m] -> [a] = m/s [g/a] = [m/s²]/[/m/s] = [1/s]

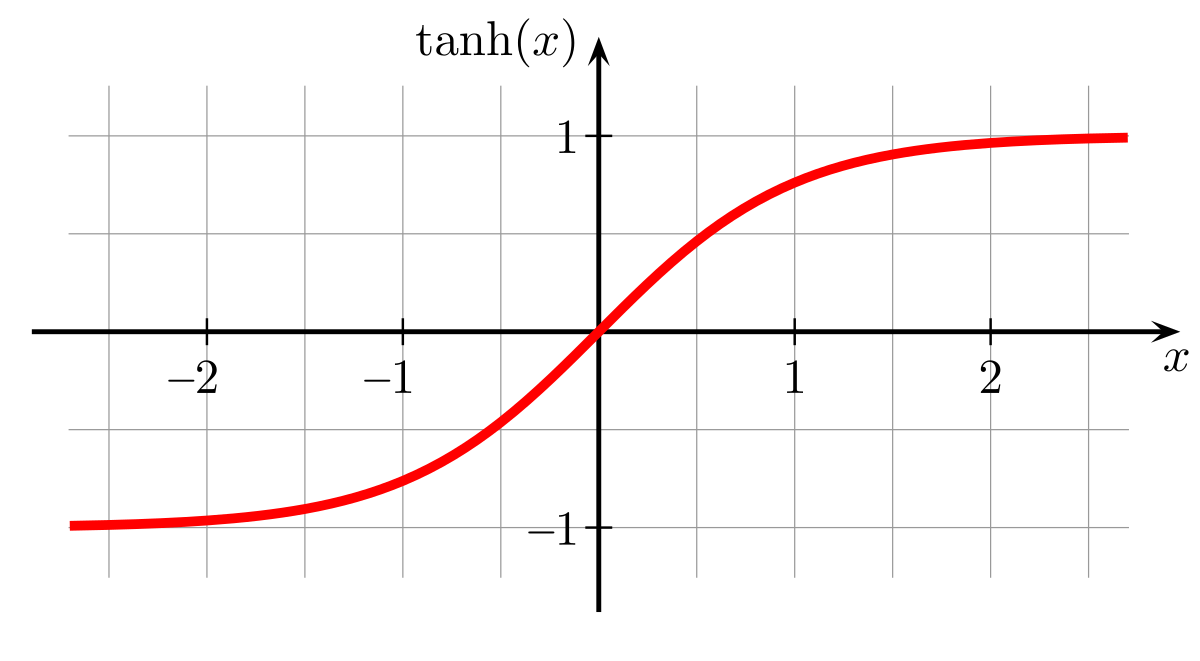
O gráfico da função tangente hiperbólico se estagna em 1 quando o argumento da função tende ao infinito. Isso significa que quando o tempo transcorrido é alto, a velocidade do corpo tente ao valor 'a', que é o mesmo da velocidade terminal calculado.