Considere o seguinte problema de valor inicial:
,
envolvendo uma equação diferencial ordinária linear de 1ª ordem não homogênea, que você irá resolver utilizando o método de variação do parâmetro.
Para isso, você começará por obter a solução geral da equação diferencial linear homogênea associada à equação diferencial dada, isto é, você irá resolver a equação diferencial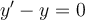 
, obtendo 
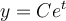, onde 
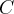é uma constante arbitrária.
Na sequência, você irá calcular uma função de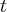 
, 
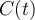, tal que 
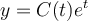seja solução geral da equação diferencial dada (não homogênea). Para isso, você substituirá na equação diferencial dada, 
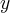por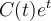 
, e conseguirá obter uma expressão para a derivada 
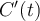, como uma função de .
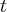O que você obtém? E para a solução deste problema de valor inicial?
; 
.
Eu consegui achar C'. No entando, eu não consegui achar esse 3e^t mas sim -e^t.
É uma derivada
