Considere que a altura de um balanço é igual a zero quando ele está em repouso. Suponha que uma
criança comece a se balançar até alcançar a maior altura que ela conseguir e que ela mantenha eu
esforço constante. A altura h(t) do assento é dada por h(t) = 8 sen (π/2t) em que t é o tempo em
segundos e h é a altura em pés. Considere que h positivo indica a altura alcançada com a criança
oscilando para frente e h negativo indica a altura alcançada com a criança oscilando para trás.
Suponha que t = 0 é quando a criança passa pela posição de equilíbrio oscilando para frente.
a) Construa o gráfico da função altura h(t) para 0 ≤ t ≤ 4.
b) Escreva uma expressão, utilizando limites e a função h(t) que represente a altura máxima atingida
pela criança.
c) Encontre a altura que a criança encontra-se do ponto mais alto do balanço.
d) Fazendo t → 0,5 s na expressão encontrada no item b, calcule a altura que a criança está.
(a) A função seno é uma função o qual temos que analizar três coisas. Argumento ( O que está dentro da função), constantes somando (O que desloca para cima e para baixo) e amplitude (O que multiplica a função e determina o tamanho da oscilação). Como no argumento só temos algo multiplicando a variável indepedente (o t), temos que o ângulo de fase (uma constante que soma no argumento) é 0. Para visualizar melhor, vamos escrever a função seno generalizada:
, Sendo A a amplitude,
a constante que multiplica t no argumento,
o ângulo de fase e c uma constante que soma na função.
Com esse argumento, sabemos que o seno, quando seu argumento é obtemos um máximo, em 0 ou
obtemos 0, em
obtemos um mínimo em um período de oscilação. Assim, quando
temos um máximo.
temos um 0.
temos um mínimo e em t=4 s outro zero. Sabemos que c=0 e A=8 pés. Portanto a função fica:
Entre em (https://www.geogebra.org/calculator) e coloque h(t)=8 sen(((?)/(2)) t) e limite seu gráfico para entre 0 e 4.
(b) Não entendi bem se esse item quer que encontre a altura máxima por limite utilizando os conceitos da função, um limite que descreva a função no ponto ou por limite fundamental achar o máximo da função. Sendo assim farei das três formas:
Máximo por limite conhecendo a função
Como vimos acima, quando t=1,3,5,7,...,2n+1, sendo , assim, podemos escrever o limite:
pés.
Limite que descreve função no ponto t-> n
Limite fundamental: (ignore caso não seja isso que tenha pedido)
A altura pode ser encontrada utilizando conceitos máximos e mínimos de cálculo diferencial (Início de calculo variacional), onde representa a inclinação de uma reta tangente a tragetória da menina. Também conhecido como definição de derivadas por limite.
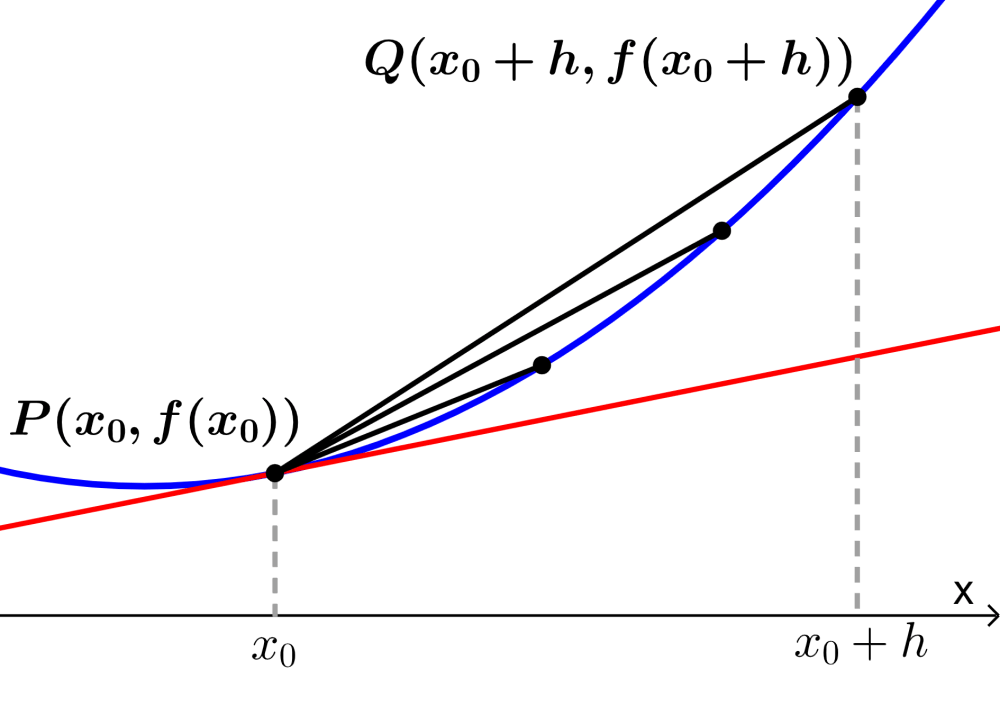
Quando a inclinação é 0, obtemos um máximo ou mínimo se a função é contínua e suave (sem bicos). Assim:
Sabemos que sen(a + b) = sen(a) · cos(b) + sen(b) · cos(a), então:
É conhecido como limite fundamental:

A parte de cosseno - 1 some naturalmente. Mas antes de aplicar o lim. fundamental, temos que fazer uma substituição . Assim, ficando:
.
Agora para achar a altura máxima basta igualar à 0. Que será quando , sendo n=0,1,2,3...
(c) Para achar a altura que a criança encontra-se do ponto mais alto, basta adicionarmos c=-8, pois, assim, no ponto mais alto encontrará-se no ponto 0 (origem). Então:
(d) Podemos substituir o valor
