Primeiro iremos definir uma função para cada deslocamento. A parte inferior se movimenta com uma velocidade constante que aqui chamaremos de . Como nós sabemos que o deslocamento gerado por uma velocidade constante é uma função linear, então o deslocamento da extremidade inferior é dado por:
Como quando ,
, então
e
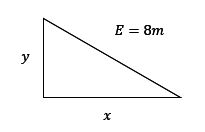
. Dito isso, outra informação dada pelo exercício é a de que o objeto é uma escada apoiada na parede, portanto, podemos dizer que as extremidades da escada e a quina da parede forma os três vértices de um triângulo retângulo. Deste modo, podemos utilizar o teorema de Pitágoras para dizer que o comprimento da escada
é igual a
onde é a distância vertical entre a extremidade superior da escada e o chão. Daqui podemos tirar que
que, por sua vez, significa que
Agora queremos descobrir a função de velocidade da descida da extremidade superior. Para isso podemos derivar a função de deslocamento pelo tempo. Para fazer isso utilizaremos a regra da cadeia para chegar a
que pode ser reduzido para
Agora precisamos descobrir em qual instante de tempo sabendo que
, nesse caso é só fazer
Sabendo que e substituindo na equação da velocidade de descida da extremidade superior, nós chegamos a
Espero ter ajudado.
Se você gostou da minha resposta, não se esqueça de vota-la.
Observação: O valor da velocidade deu negativo porque a distância entre a extremidade superior da escada e o chão está decrescendo com o tempo e é por isso que essa derivada dá um valor negativo.

Dados do problema:
Você pode observar que h é a altura da escada (hipotenusa) e a taxa de variação (velocidade) da posição da extremidade inferior ou pé da escada x(t), medida a partir da parede ao longo da direção x. Ou seja, conforme o pé da escada tende a se afastar da parede, observamos um movimento correspondente do topo da escada que vem em direção ao chão. Isso acontece porque h é sempre constante (o tamanho da escada é fixo) e mantemos o topo fixado na parede, de modo que apenas o pé da escada "escorrega" para frente, enquanto o topo "escorrega" para baixo.
Pergunta: qual a velocidade do topo da escada quando x(t) = 3 m?
A função que utilizamos é a relação de Pitágoras , dado que a escada sempre forma um triângulo retângulo com uma parede vertical.
Substituindo h=5, então
Podemos aplicar a derivada temporal na equação para conhecer suas taxas de variação:
Não conhecemos a dependência de x e y com relação ao tempo (é isso que precisamos determinar), mas podemos utilizar a regra da cadeia para isolar e
na equação, e encontrar sua dependência de x e y.
Nessa equação diferencial podemos ver que a relação das velocidades das extremidades da escada é negativa, pois a velocidade do topo está contrária ao sistema de referências adotado (y para cima). Outra constatação é que quanto mais o movimento composto avança no tempo, a velocidade do topo aumenta devido a x, mas se reduz devido a y, mantendo-se estável (o que significa que ela não vai tender ao infinito negativo quando y chegar a 0.
O próximo passo seria substituir para encontrar , mas não temos o valor de y. Vamos resolver a identidade de Pitágoras, primeiro, no ponto x = 3 m. Lembrando que x(t) é a distância do pé da escada em um dado instante e y(t) a altura do topo.
Logo:
Espero que ter esclarecido a dúvida. Até mais.
