Representando por 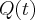 a quantidade
a quantidade  de material radioativo em certo instante de tempo
de material radioativo em certo instante de tempo 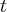
 , sabe-se que ela decai a uma taxa proporcional à quantidade presente, de acordo com a equação
, sabe-se que ela decai a uma taxa proporcional à quantidade presente, de acordo com a equação
onde  , denominada constante de decaimento, é uma constante positiva
, denominada constante de decaimento, é uma constante positiva 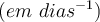 .
.
Determine, em dias, o tempo 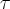 que leva para uma quantidade decair para
que leva para uma quantidade decair para 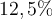 da quantidade inicial
da quantidade inicial 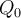 mg, isto é,
mg, isto é,  de
de 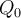 mg.
mg.
A equação diferencial é
Separando as variáveis temos
Integrando ambos os membros obtemos
em que C é a constante de integração. Aplicando a função exponencial em ambos os membros obtemos
Para t=0 temos . Portanto
.
Para o tempo ocorre o decaimento para a quantidade
. Então substituindo estes dados na equação acima:
Portanto o decaimento para 12,5% ocorre após dias.

