Estatistica 000000

Olá! Vamos lá!! Primeiro temos que saber quais são as informações: temos que o peso segue uma distribuição normal, temos a média, o desvio padrão e o valor limite, com isso conseguimos usar a padronização Z que tem fórmula:

onde o é o desvio padrão e a média.

Então, queremos saber quando o peso passa dos 650kg. Para isso precisamos achar qual é o Z de 650kg, isto é, precisamos substituir o X por 650. Assim colocando os valores na fórmula temos:

Agora chegou a parte que vc precisa tomar cuidado que é a parte de olhar as tabelas relacionadas a distribuição. Existem vários tipos de tabelas que podem contar do centro da distribuição até uma extremidade ou até mesmo de uma extremidade até algum ponto, então sempre olhe como é a figura que está em cima da tabela (que geralmente tem)

Essa daqui, por exemplo mostra o valor da área de Z de uma ponta até um outro ponto qualquer. Sabendo que a probabilidade é a área do gráfico e que temos o Zp indicado, então, essa tabela mostra a chance de ser menor que 0,625 e por sua vez menor que 650kg. Assim para saber quais são os valores maiores basta efetuar uma subtração, pois sabemos que a área total disso é 1.

Antes disso vamos achar o valor da probabilidade para o Z=0,625. A coluna da esquerda irá mostrar a primeira casa decimal, enquanto a linha mostra a segunda. Arredondando Z apra 0,63, podemos achar que a chance é de 0,7324 (6 linha, 4 coluna). Escrevendo em matematiques:

Traduzindo, a probabilidade de o peso da carga ser maior que 650 é a mesma coisa que a probabilidade de Z ser maior que 0,625. Sabendo que a probabilidade de Z ser menor que 0,625 é de 0,7324, então se eu fizer 1-0,7324, saberei qual é a probabilidade de ser maior, pois 0,7324 mais a probabilidade de ser maior que 0,625 tem que ser 1. Então, no final, essa chance é de 0,2676 ou 26,76%.

Mas Sammer, achei muito difícil! Não tem problema, podemos procurar uma tabela que vai nos dar exatamente esse valor, que é essa daqui: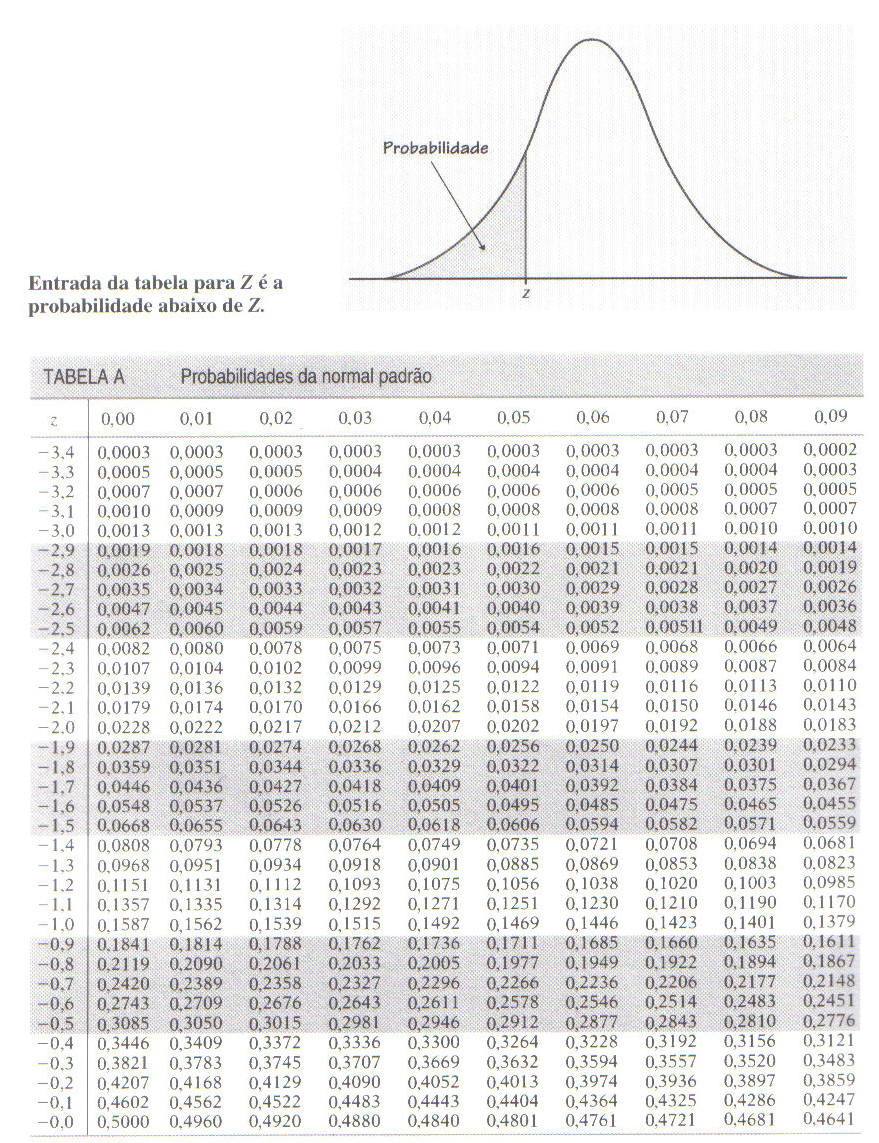

Mas Sammer, essa tabela não é a mesma da outra? Basicamente, sim. Só está mostrando os valores negativos. Como sabemos que a distribuição é simétrica, isso quer dizer que o que vale para um lado, vale para outro. Assim a probabilidade do valor ser menor que -0,650 é igual a probabilidade do valor ser maior que 0,650. Ou seja:

Assim, nessa tabela basta olhar o valor de -0,625, que arredondanto para -0,63 dará 0,2676 .

É isso! Espero que tenha entendido :)