Em uma polia de massa desprezível e sem atrito, o corpo A possui massa 5 kg. Qual a massa do corpo B que desce com movimento acelerado e aceleração de módulo 5 m/s². Adote g = 10 m/s².
a) 10kg
b) 15 kg
c) 20 kg
d) 25 kg
e) 30 kg
Bom dia Camila. Vamos lá:
Aplicação da segunda lei de Newton para o corpo A que está subindo:
T(tensão na corda) - Pa(peso do corpo A) = ma*a
Aplicação da segunda lei de Newton para o corpo B que está descendo:
Pb(Peso do corpo B) - T(tensão na corda) = mb*a
Portanto, temos um sistema de 2 equações que vamos resolver pelo metodo da adição:
T - Pa = ma*a (I)
Pb - T = mb*a (II)
________________ (I) + (II)
Pb - Pa = (mb + ma ) * a; vamos substituir os valores numericos dados no problema e encontrar mb:
mb*10 - 5*10 = (mb + 5 ) * 5--------->mb*10 - 50 = 5*mb + 25---------->5*mb = 75----->mb = 15 kg.
Portanto, a alternativa correta é a b).
Sucesso!!!!!!!!!!!!!


Parece-me que é 15 kg, letra b.

Olá, Camila.
Aqui a massa de b deu 15kg, alternativa b)

Pela segunda lei de Newton:
Somando (1) e (2):

Este sistema é chamado de Máquina de Atwood.
Pelo enunciado, o corpo B desce, consequentemente a sua massa é maior que a massa do corpo A.
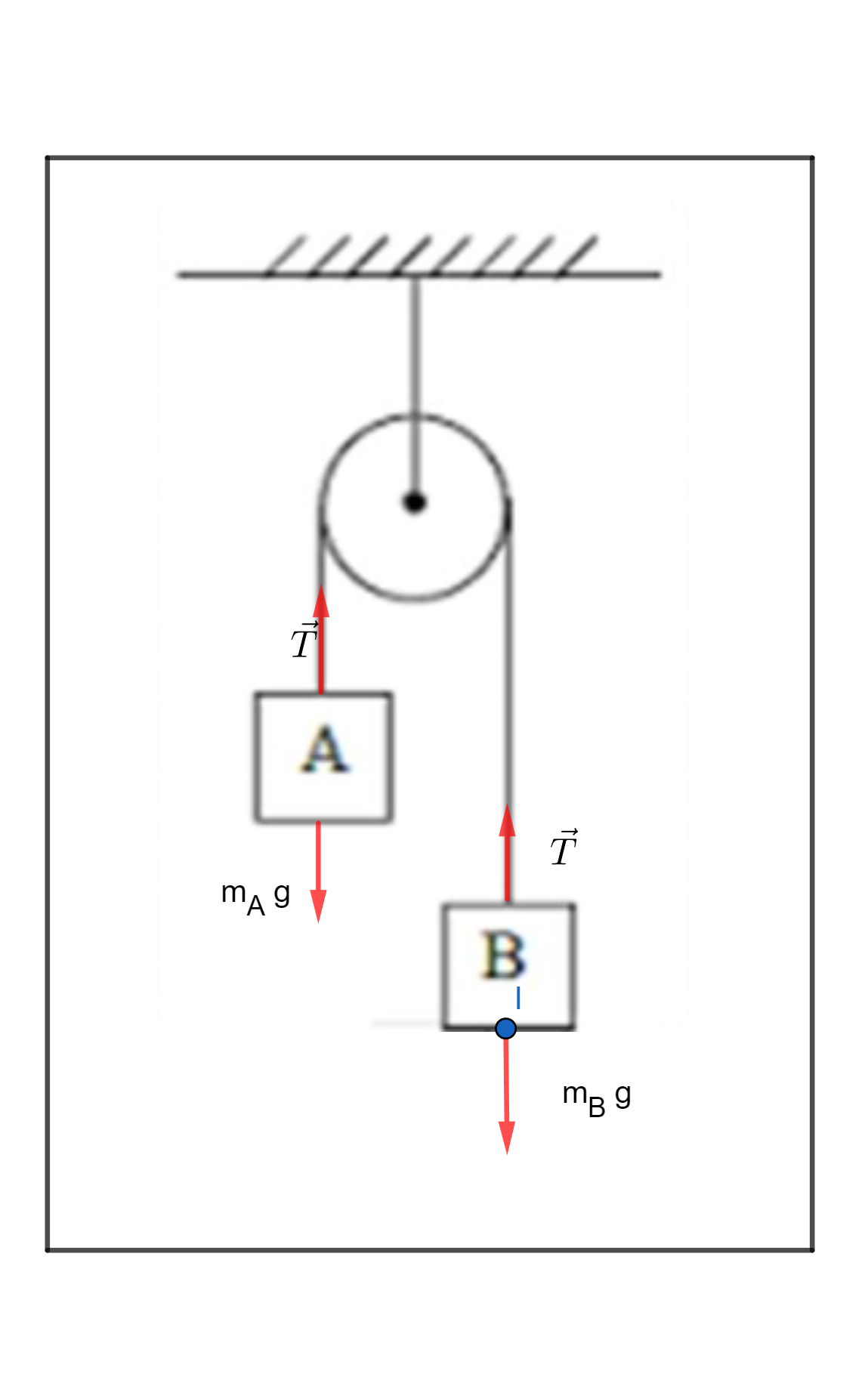
Vejamos as forças que atuam no sistema, considerado no enunciado ideal desde desprezamos a massa da polia e da corda e também consideramos que não existe atrito:
No bloco A:
Para baixo: Peso de A = PA
Para cima: Tração na Corda: T
No bloco B:
Para baixo: Peso de B = PB
Para cima: Tração na Corda: T
Aplicando a 2a Lei de Newton, temos:
PB - PA = (mA + mB).a
mB.g - mA.g = (mA + mB).a
10mB - 5.10 = (5 + mB).5
10mB - 50 = 25 + 5mB
10mB - 5mB = 25 + 50
5mB = 75
mB = 75/5
mB = 15 kg
Espero ter ajudado!
