Questão de física/magnetismo

Acho que essa questão caiu na internet errada e já foi até resolvida no Brainly. O enunciado não faz muito sentido e, quanto às alternativas, veremos que possuem a escala errada. 

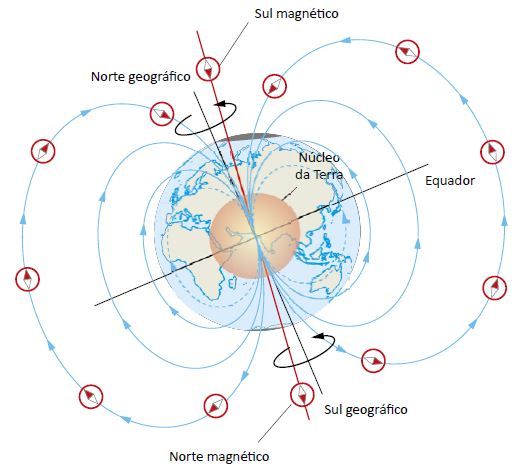
Primeiro, vamos considerar que a densidade de campo magnético da Terra seja mesmo de 50 ou 0,05 . Esse dado já está mal contextualizado, por causa da forma do campo magnético da Terra. O campo magnético da Terra é formado por linhas de campo, descritas por vetores variados pontualmente ao longo da linha. Quando utilizamos uma bússola, o Sul Magnético atrai a Ponta Norte da bússola (e a recíproca também é verdadeira), de forma que a bússola se alinha perfeitamente a reta que tange a linha de campo naquele ponto. A consequência prática disso é que o imã da bússola "aponta" para o Norte Geográfico. Assim, dizemos que o sentido do campo na superfície terrestre é invariavelmente "virado para o Norte", como mostra a Figura 1.

Figura 1 - Sentido do Campo Magnético da Terra

Fonte: Projeto Física e Cidadania

Basicamente, o vetor densidade de campo aponta na direção tangente à linha de campo, que nem sempre é paralela à superfície terrestre. Nesse caso, pegamos sua componente paralela (). Mas vamos assumir que o campo seja paralelo à superfície e aponte para o Norte Geográfico como indica a Figura 2 para a região do Equador. Então podemos dizer que e . Levando isso em conta, o campo magnético resultante da soma vetorial do campo magnético terrestre com o campo devido à corrente no condutor não poderia ser menor que 50 no plano horizontal. Vamos verificar a justificativa para isso mais adiante.

Figura 2 - Direção do Campo em relação à Superfície Terrestre

Fonte: Cola da Web

Segue o link para mais esclarecimentos sobre essa questão: Física UFMG.

Com essa ressalva em mente, podemos calcular a densidade de campo devido à corrente constante passando em um condutor retilíneo.  Essa grandeza pode ser determinada experimentalmente de acordo com a Lei de Biot-Savart. Nesse momento, é mais didático representar as grandezas vetoriais por meio de um diagrama:

Figura 3 - Lei de Biot-Savart

Fonte: Magnetismo na Web

Na prática, a magnitude de é diretamente proporcional a um certo trecho de comprimento do condutor e inversamente proporcional ao quadrado da distância entre a posição desse trecho e um ponto qualquer do plano, genericamente chamado de . Sem esquecer que é função da corrente constante e da proporcionalidade das dimensões, tem-se:

Isso pode ser simplificado decompondo a distância  em sua componente na direção de :

O passo a seguir envolve um pouco de Cálculo Vetorial, então não tem problema se passar como um furacão pela sua cabeça. Apenas aperte o cinto que já vamos pousar em segurança. Como uma idealização do problema, admitimos que o condutor seja infinito, no sentido de que seu comprimento é indescritivelmente maior do que a distância , o que virtualmente coloca  muito próximo de . Mas por que ? É a pulga que deve estar beliscando a sua orelha nesse momento. Porque  nada mais é do que duas vezes , quando estendemos o trecho "" para compreender o condutor desde até o Norte infinitamente, e depois até o Sul infinitamente, partindo também de P. Então, usando um pouco de limite, quando , e . Se , também implica que e .

Moral da história: não pode depender nem de , nem de , pois a relação desses valores se torna desprezível, assim:

Que é a forma mais conhecida e aplicada da Lei de Biot-Savart no Ensino Médio. Lembrando que este é um caso ideal e muito particular do campo produzido pela corrente que circula em um condutor, podemos resolver o exercício substituindo os dados a seguir na fórmula:

; ;

Finalmente, retornamos à justificativa quanto ao erro do enunciado. Existem dois campos magnéticos se sobrepondo no plano da superfície terrestre. Um de 50 "micro" Teslas e outro de 30. Isso nos dá 3 resultados possíveis: ou os campos estão na mesma direção e sentido e se somam (campo total igual a 80), estão em sentidos opostos, na mesma direção e se cancelam (campo total igual 20). A terceira opção seria uma combinação das duas primeiras e aí você precisa decompor os dois vetores em um sistema de eixos comuns e somar componente a componente. Vamos analisar esse caso com mais detalhes a seguir.

Para deduzir a direção e sentido do campo devido à corrente no condutor, utilizamos a Regra da Mão Direita:

Figura 4 - Direção do Campo devido à Corrente no Fio

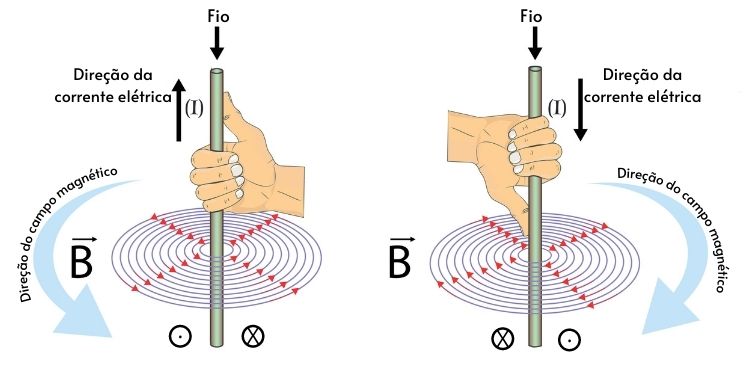
Fonte: PreparaEnem

Assumindo que o plano da superfície terrestre seja o mesmo da folha, verificamos que a corrente seguindo no sentido de Norte-Sul equivale a uma corrente descendo pelo condutor. O campo emitido por essa corrente é composto por linhas concêntricas e, do mesmo modo que o campo magnético da Terra, tem direção da tangente em cada ponto dessas linhas. Nesse contexto, o lado esquerdo da folha representa o Oeste, assim como o lado direito representa o Leste. Se a corrente circula no fio de cima para baixo, utilizando a Regra da Mão Direita, podemos concluir que o campo magnético entra na folha pela esquerda e sai pela direita. Agora vamos imaginar que estamos olhando para a Terra do espaço em vez de para a mão de um cara aleatório na internet. Alinhando o fio com os polos geográficos, verificamos que as linhas de campo que penetram a superfície logo abaixo do condutor, estão indo na direção equatorial, do Oeste para o Leste (da esquerda para a direita).

Se sobrepormos a Figura 4 com a Figura 1 ou a 2, fica justificado porque o campo magnético resultante deve ser necessariamente maior do que o campo magnético terrestre: os dois vetores são perpendiculares entre si, formando um triângulo retângulo, cuja resultante pode ser determinada pelo Teorema de Pitágoras (). Como é um caso muito particular, não tenho como lhe oferecer uma figura ilustrativa, mas fica o desenho do diagrama vetorial como lição de casa.

Feito isso, tente algumas variações do problema:

a) Tente verificar como os dois campos são perpendiculares entre si e enxergar a resultante dos dois tendo a Terra como plano de fundo. É interessante observar como a resultante se aproxima da direção Norte-Sul conforme o campo devido à corrente diminui, e como se aproxima da direção Oeste-Leste conforme esse mesmo campo cresce. Enfim, uma ótima aplicação de componentes vetoriais.

b) Veja também o que acontece se trocarmos o sentido da corrente para "subir" no plano da folha, ou seja, para ir em sentido ao Norte Geográfico.

c) Finalmente, tente imaginar qual deveria ser a direção do condutor para produzir um campo cuja resultante fosse, de fato, menor do que uma de suas componentes, no caso, o campo magnético da Terra. Dica: basta colocar os dois campos na mesma direção e sentidos opostos.