Os materiais, nas mais diversas formas de componentes que eles podem assumir, sofrem variados tipos de esforços quando estão em operação. Além disso, cada material possui características próprias como por exemplo: o ferro fundido é duro e frágil, o aço é bastante resistente, o vidro é transparente e frágil, o plástico é impermeável, a borracha é elástica etc. Dureza, fragilidade, resistência a fluência, resistência a tração e ductilidade são exemplos de propriedades mecânicas dos materiais. Uma empresa solicitou teste de tração para um material comprado por suspeitar que os valores das propriedades desse material não condiziam com o material recebido. O resultado do teste é apresentado no gráfico de tensão-deformação abaixo.
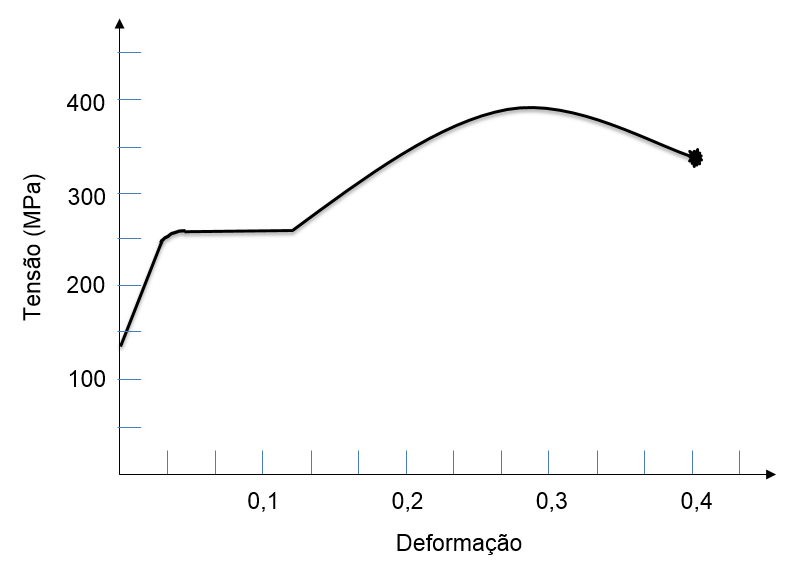
?A partir dos dados do diagrama de tensão-deformação do material comprado, verifique se as informações passadas pelo vendedor são verídicas ou não. Dados fornecidos pelo vendedor:

Olá, Aline!
A definição para "limite de escoamento" está relacionada com o limite de proporcionalidade, que corresponde ao ponto onde ocorre o afastamento da linearidade na curva tensão-deformação.
No gráfico, isso acontece para o valor de tensão igual a 250 MPa.
A definição para "limite de resistência à tração" está relacionada com o que ocorre após o escoamento, em que a tensão necessária para continuar a deformação plástica aumenta até um valor máximo, que corresponde ao limite de resistência à tração, e então diminui até a fratura do material.
No gráfico, isso acontece para o valor de tensão igual a 400 MPa.
Portanto, a partir dos dados do diagrama de tensão-deformação do material comprado, as informações passadas pelo vendedor não são verídicas, ou seja, são falsas!
Bons estudos!!

boa tarde
2 Conceitos de tensão e deformação Se uma carga é estática ou se ela se altera de uma maneira relativamente lenta ao longo do tempo e é aplicada uniformemente sobre uma seção reta ou superfície de um membro, o comportamento mecânico pode ser verificado mediante um simples ensaio de tensão-deformação. Existem três maneiras principais segundo uma carga pode ser aplicada: tração, compressão e cisalhamento. Em engenharia, muitas cargas são de natureza torcional, e não de natureza puramente cisalhante. 2.3 Discordâncias e sistemas de escorregamento Discordâncias existem em materiais cristalinos devido às imperfeições no cristal. Essas imperfeições possibilitam o escorregamento de planos dentro do cristal. A movimentação de discordâncias é o principal fator envolvido na deformação plástica de metais e ligas. A mobilidade de discordâncias pode ser alterada por diversos fatores (composição, processamento…) manipulação das propriedades mecânicas do material. E as discordâncias também afetam outras propriedades do material, além das mecânicas. Como a condutividade em materiais semicondutores. No nosso estudo vale ressaltar: nos materiais cristalinos o principal mecanismo de deformação plástica geralmente consiste no escorregamento de planos atômicos através da movimentação de discordâncias. Na Figura 1 são ilustrados os sistemas de escorregamento. Figura 1 - Sistemas de escorregamento. As discordâncias não se movem com a mesma facilidade em todos os planos cristalinos e em todas as direções cristalinas. A movimentação das discordâncias se dá preferencialmente através de planos específicos e, dentro desses planos, em direções específicas, ambos com a maior densidade atômica de um dado reticulado cristalino. Essa combinação de um plano e uma direção é chamada de sistema de escorregamento (“slip system”). 11 Um sistema de escorregamento é definido por um plano e por uma direção de escorregamento, ambos com a maior densidade atômica em um dado reticulado cristalino. 2.4 Deformação elástica O grau ao qual uma estrutura se deforma ou se esforça depende da magnitude da tensão imposta. Para a maioria dos metais que são submetidos a uma tensão de tração em níveis baixos, são proporcionais entre si: ? ? E.? Esta relação é conhecida por lei de Hooke, e a constante de proporcionalidade E (GPa ou psi) é o módulo de elasticidade, ou módulo de Young. O processo de deformação no qual a tensão e a deformação são proporcionais entre si é chamada de deformação-elástica, com o gráfico de ?x? resultando em uma reta, conforme mostrado na Figura 2. Figura 2 - Lei de Hooke. Porém a lei de Hooke não é válida para todos os valores de deformação, ela é uma aproximação quando a tensão é relativamente baixa. Também, a deformação elástica não é permanente o que significa que quando a carga aplicada é liberada, a peça retorna a sua forma original. Em uma escala atômica, a deformação elástica macroscópica é manifestada como pequenas alterações no espaçamento interatômico e na extensão das ligações interatômicas. Como conseqüência, a magnitude do módulo de elasticidade representa uma medida da resistência à separação de átomos adjacentes, isto é, as forças de ligação interatômicas. Tabela 1 - Módulos de elasticidade, de cisalhamento e coeficiente de Poisson para algumas ligas metálicas. Os valores dos módulos de elasticidade para materiais cerâmicos são características maiores do que para os metais, e para os polímeros são menores. Essas diferenças são consequências diretas dos diferentes tipos de ligação atômica nesses três tipos de materiais. Ademais, com o aumento da temperatura, o módulo de elasticidade tende a diminuir. 12 A imposição de tensões compressivas, de cisalhamento ou torcionais também induzem um comportamento elástico. As características tensão-deformação a baixos níveis de tensão são as mesmas¸ tanto para uma situação de tração quando de compressão, proporcionais ao módulo de elasticidade. A tensão e a deformação de cisalhamento são proporcionais uma à outra através da seguinte expressão: ? ? G.? onde G representa o módulo de cisalhamento. Exemplo 1 Uma barra de aço 1040 de diâmetro 10mm, cujo módulo de elasticidade é 200GPa se submete a uma carga C pressão de tensão de 50.000N levando-la um pouco mais do seu limite de proporcionalidade. Calcule a recuperação elástica que ocorre uma vez eliminada a tensão. Calcule a tensão S P ? ? MPa m N 637.10 637 .(5.10 ) 50000. 6 3 2 ? ? ? ? ? ? Entre Y.S (600MPa) e T.S (750MPa) Recuperação Elástica 3 9 6 3,19. 200.10 637.10 ? ? ? ? Pa Pa E ? ? 2.5 Deformação plástica Para a maioria dos materiais metálicos, o regime elástico persiste até deformações de aproximadamente 0,005. A medida que o material é deformado além desse ponto, a tensão não é mais proporcional à deformação, ocorrendo então uma deformação permanente não recuperável, ou, deformação plástica. (A lei de Hooke não é mais válida). A Figura 3 mostra os gráficos de tensão x deformação típicos para alguns tipos de aço. Percebe-se que a baixas tensões existe uma região linear, que aos poucos entra em uma região não-linear, a chamada região de deformação plástica. Figura 3 - Gráfico tensão x deformação para deformação plástica. 13 A partir de uma perspectiva atômica, a deformação plástica corresponde à quebra de ligações com os átomos vizinhos originais e em seguida formação de novas ligações com novos átomos vizinhos, uma vez que um grande número de átomos ou moléculas se move em relação uns aos outros; com a remoção da tensão, eles não retornam ás suas posições originais. O mecanismo dessa deformação é diferente para materiais cristalinos amorfos. No caso de sólidos cristalinos, a deformação ocorre mediante um processo chamado de escorregamento, que envolve o movimento de discordâncias. 2.6 Tensão nominal e deformação nominal Também chamados de tensão de engenharia e deformação de engenharia. Quando é feito um ensaio de tração, as grandezas que são medidas são a força aplicada (carga) e o alongamento da peça. Para se encontrar a tensão precisa-se levar em conta a área do corpo de prova. O problema é que durante o ensaio, a seção reta do corpo de prova diminui, devido ao alongamento do mesmo, dificultando a medição da tensão. Para isso utiliza-se a tensão nominal e deformação nominal. Que são calculados a partir da área inicial, considerando que ela se mantenha constante durante todo o ensaio. 2.6.1 Tensão nominal A tensão de engenharia, ou tensão nominal, como definida anteriormente, é representada pelo caractere ?, e é definida pela relação: AO F ? ? sendo: ? a tensão (em MPa), F a força aplicada e AO a área da seção inicial do corpo onde é diretamente aplicada a carga. 2.6.2 Deformação nominal A deformação nominal, ou deformação de engenharia, como foi definido anteriormente, é representada pelo caractere ?, e é definida pela relação: O O O i L L L L L ? ? ? ? ? sendo: LO o comprimento original antes de ser aplicada carga e Li o comprimento instantâneo antes de ser aplicada carga. Algumas vezes a grandeza LO - Li é substituída por ?L, e representa o alongamento da deformação ou variação no comprimento a um dado instante, conforme referência ao comprimento original. 2.7 Ensaio de tração Um dos ensaios mecânicos de tensão-deformação mais comuns é executado sobre tração. Como será visto, o ensaio de tração pode ser usado para avaliar diversas propriedades mecânicas dos materiais que são importantes em projetos. 14 Uma amostra é deformada, geralmente até sua fratura, mediante uma carga de tração gradativamente crescente, que é aplicada uniaxialmente ao longo do eixo mais comprido de um corpo de prova. Normalmente a seção reta é circular, porém corpos de prova retangulares também são usados. Durante os ensaios, a deformação fica confinada a região central, mais estreita do corpo de prova, que possui uma seção reta uniforme ao longo do seu comprimento. O corpo de prova é preso pelas suas extremidades nas garras de fixação do dispositivo de testes. A maquina de ensaios de tração alonga o corpo de prova a uma taxa constante, e também mede contínua e simultaneamente a carga e os alongamentos resultantes. Tipicamente, um ensaio de tensãodeformação leva vários minutos para ser executado e é destrutivo, isto é, até a ruptura do corpo de prova. Figura 4 - Corpo de prova padrão para ensaio de tração. Os resultados de um ensaio de tração são anotados em um gráfico de tensão x deformação (Figura 5). Figura 5 - Gráfico tensão nominal x deformação nominal. Como visto, a relação entre tensão, força aplicada e a área da seção: Ao F ? ? Em ensaios de tração convencionou-se que área da seção utilizada para os cálculos é a da seção inicial (AO). Aplicando essa relação obtêm-se os valores de tensão que relatados num gráfico demonstram as relações entre tensão nominal e deformação nominal no decorrer do ensaio. 15 2.7.1 Valores das propriedades mecânicas obtidas a partir do ensaio de tração e diagrama tensão nominal-deformação nominal A partir de um gráfico de tensão x deformação é possível obter muitas propriedades sobre o material. A seguir, nas Figuras 6 e 7, serão mostrados os gráficos de dois grupos de materiais, os materiais dúcteis e os materiais frágeis. Materiais dúcteis têm a propriedades de que quando estão sob a ação de uma força, podem estirar-se sem romper-se, transformando-se num fio. Exemplos de materiais dúcteis são o ouro, o cobre e o alumínio. Por outro lado, um material frágil é um material que não pode se deformar muito. Com deformações relativamente baixas o material já se rompe. Um exemplo de material frágil é o vidro. As propriedades desses materiais obtidas a partir de um diagrama de tensão x deformação são mostradas a seguir: ? Materiais dúcteis (aço estrutural e outros metais): ?u: tensão última (máxima tensão que se atinge) ?R: tensão de ruptura (tensão que, se atingida, provoca a ruptura do material) ?e: tensão de escoamento ?R: deformação de ruptura (deformação que, se atingida, provoca a ruptura do material) Figura 6 - Diagrama ?x ? para material dúctil. Fases de evolução do diagrama (Figura 6): 1. Aumento lento do comprimento (pequena deformação), diretamente proporcional a uma grande carga aplicada (trecho reto da origem até a tensão de escoamento - ?e), com grande coeficiente angular (reta "quase" na vertical). 2. Longa deformação com pouco aumento da carga aplicada, ou seja, pequena variação da tensão (escoamento). 3. Aumento da deformação proporcional ao aumento da carga aplicada, ou seja, da tensão. Este aumento ocorre até que a carga aplicada atinja um valor máximo, ou, uma tensão última - ?u (recuperação). 4. Diminuição do diâmetro do corpo (estricção). Uma diminuição da carga aplicada é suficiente para manter a deformação até a ruptura. (?R: tensão de ruptura; ?R: deformação de ruptura). 16 ? Materiais frágeis (ferro fundido, vidro, pedra...): ?u: tensão última (máxima tensão que se atinge) ?R: tensão de ruptura (tensão que, se atingida, provoca a ruptura do material) ??R: deformação de ruptura (deformação que, se atingida, provoca a ruptura do material) Figura 7 - Diagrama ?x ?para material frágil. Evolução do diagrama (Figura 7): aumento da deformação proporcional ao aumento da carga aplicada até que se atinja a deformação de ruptura (?R) que corresponde à tensão de ruptura (?R) que é igual à tensão última (?u). Módulo de elasticidade: O módulo de elasticidade, denotado por ?, é obtido na parte linear dos gráficos, sendo mais evidente para o material dúctil. A região linear é parte que vai do valor zero, até o valor de ?e (tensão de escoamento). Ao obter o valor numérico referente a inclinação dessa reta se obtém o valor de ?. Tensão de escoamento: Existente somente para o material dúctil, e marca o ponto onde o material entra na região de escoamento. Esse fenômeno, nitidamente observado em metais de natureza dúctil, como aços baixo teor de carbono e caracteriza-se por um grande alongamento sem acréscimo de carga. Tensão de ruptura: ?R , como o próprio nome já diz, é a tensão com a qual o material se rompe. Porém é importante observar que nem sempre a tensão de ruptura é a tensão máxima que pode ser aplicada. Ao observar a Figura 6, percebe-se que o material pode chegar ao mesmo nível da tensão de ruptura e mesmo assim não se romper. Ele somente se rompe se tensão máxima já tiver sido ultrapassada, e então o material se alongaria novamente até romper, com um decréscimo na tensão, chegando em ?R. Alongamento percentual: O alongamento percentual AL% é porcentagem da deformação plástica quando do momento da fratura, ou % .100 ? ?.100 ? ? O f O L L L AL onde Lf representa o comprimento no momento da fratura e LO representa o comprimento original. Uma vez que uma proporção significativa da deformação plástica no momento da fratura está confinada à região do pescoço, a magnitude do AL% dependerá do comprimento útil do corpo de prova. Esse alongamento é muito mais evidente em materiais dúcteis, como pode ser observador na Figura 8, e ele serve para determinar a ductilidade em termos do alongamento. 17 Figura 8 – Diagrama ? x ?, evidenciando a ductibilidade. Percentagem de redução da área: Semelhante ao alongamento percentual, também é uma medida que pode definir a ductibilidade do material, porém medindo se a área. É definida por: % .100 O O i A A A RA ? ? sendo AO a área original da seção reta e Ai a área da seção reta no momento da fratura A maioria dos materiais possui pelo menos um grau modulado de ductibilidade a temperatura ambiente, contudo, alguns se tornam frágeis à medida que a temperatura é reduzida. 2.8 Resistência à fratura A resistência à fratura de um material é determinada pela tenacidade. A tenacidade é um termo mecânico que é usado em vários contextos: livremente falando, ela representa uma medida da habilidade de um material em absorver energia até sua fratura. Para uma situação estática (pequena taxa de deformação), a tenacidade pode ser determinada a partir dos resultados de um ensaio tensão-deformação. Ela é a área sob a curva ?x? até o ponto de fratura. As unidades de tenacidade são: energia por unidade de volume do material. Para que um material seja tenaz, ele deve apresentar tanto resistência como ductibilidade. E freqüentemente materiais dúcteis são mais tenazes que materiais frágeis. 2.9 Ensaio de flexão O ensaio de flexão foi adotado com o objetivo de ser utilizado em materiais frágeis para determinar a tensão e flecha de ruptura, e também permitir avaliar outras propriedades mecânicas, como o módulo de elasticidade à flexão. A técnica de ensaio consiste em apoiar o corpo de prova em dois pontos distanciados de um comprimento (L) e aplicar lentamente uma força de flexão (F) no centro deste. Figura 9 - Ensaio de flexão. 18 Deste ensaio pode ainda retirar-se o módulo de ruptura (Mr), que significa o valor máximo da tensão de tração ou de compressão nas fibras externas do corpo de prova e que pode ser obtido pela a seguinte expressão: I Y M M r r . ? onde, M é o momento máximo de flexão igual a (FmaxL/2) expresso em [Nmm-2 ], Y é a distância do eixo à fibra externa em mm e I o momento de inércia inicial da secção transversal do corpo de prova em relação ao seu eixo, em mm4 . Outra propriedade possível de obter no ensaio de flexão é o módulo de elasticidade à flexão (E) através da seguinte expressão: Y I F L E 48. . . 3 ? em que, Y é a flecha medida para a força (F) aplicada a meio vão, L é o tamanho do corpo de prova e I é o momento de inércia. Os momentos de inércia do corpo de prova podem ser calculados a partir de sua geometria: 64 .d I ? ? para seção circular, e 12 . 3 b h I ? para seção retangular. A grande vantagem do ensaio de flexão é a de permitir utilizar corpos de prova mais fáceis de preparar do que os corpos de prova para o ensaio de tração, tem mais aplicação quanto mais duro for o material. No entanto, para materiais muito frágeis, os resultados obtidos apresentam grande dispersão, de modo que nestes casos devem realizar-se sempre vários ensaios para estabelecer um valor médio.
segundo o PROF.fABIO
