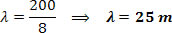um pulso ondulatório transversal é produzido em uma corda homogênea de massa igual a 500g e de 0,5 m de comprimento, esticada horizontalmente. sabendo que a tensão da corda é 10.000 n qual a velocidade da propagação no pulso da corda? a) 100 m/s b) 10 m/s c) 50 m/s d) 200 m/s
A velocidade de um pulso transversal em uma corda por meio de uma força pode ser obtida pela Fórmula de Taylor:
v = raiz(F/p) em que "F" é a força e "p" a densidade linear obtida como sendo o quociente entre massa/comprimento, ou seja, m/L.
Portanto substituindo na expressão acima:
v = raiz(F*L/m) = raiz(10000*0,5/0,5) = raiz(10000) = 100m/s. Alternativa A
Lembre-se que as unidade devem estar no sistema internacional de medidas. Ou seja a massa 500g = 0,5Kg e o comprimento 50cm = 0,5m.
Obs: raiz significa a raiz quadrada da expressão entre parenteses.


Questão 1
(Mackenzie SP/2006) As antenas das emissoras de rádio emitem ondas eletromagnéticas que se propagam na atmosfera com a velocidade da luz (3,0.105 km/s) e com frequências que variam de uma estação para a outra. A rádio CBN emite uma onda de frequência 90,5 MHz e comprimento de onda aproximadamente igual a:
a) 2,8 m
b) 3,3 m
c) 4,2 m
d) 4,9 m
e) 5,2 m
Questão 2
(Unifor/CE/Janeiro/Conh. Gerais/2001) Na figura está representada a configuração de uma onda mecânica que se propaga com velocidade de 20 m/s.

A frequência da onda, em hertz, vale:
a) 5,0
b) 10
c) 20
d) 25
e) 50
Questão 3
É correto afirmar sobre as ondas mecânicas:
a) transportam massa e energia
b) transportam massa e quantidade de movimento
c) transportam matéria
d) Transportam energia e quantidade de movimento
e) Nda
Questão 4
Suponha uma corda de 10 m de comprimento e massa igual a 500 g. Uma força de intensidade 300 N a traciona, determine a velocidade de propagação de um pulso nessa corda.
Respostas
Resposta Questão 1
f = 90,5 MHz = 90,5 . 106 Hz
Velocidade da luz (c) = 3,0 . 105 km/s = 3,0 . 108 m/s
Podemos utilizar a equação: v = ? . f, mas nesse caso trocaremos “v” por “c” por se tratar da velocidade da luz. Logo: c = ? . f
3,0 . 108 = ? . 90,5 . 106
? = 3,0 . 108
90,5.106
? = 0,033 . 108-6 = 0,033 . 10²
? = 3,3 m
Alternativa “b”.
Resposta Questão 2
Pela figura podemos perceber que ? = 20 cm
4
Logo ? = 80 cm = 0,8 m
Como v = ? . f e sabendo que v = 20 m/s, temos: 20 = 0,8 . f
f = 20
0,8
f = 25 Hz
Alternativa “d”
Resposta Questão 3
As ondas mecânicas são perturbações de um meio material elástico que se propagam por esse meio, transportando energia e quantidade de movimento.
Portanto, na propagação das ondas há transporte de energia e quantidade de movimento.
Alternativa “d”.
Resposta Questão 4
O comprimento da corda (L) = 10 m
m = 500 g = 0,5 kg
? = m
L
? = 0,5
10
? = 0,05 kg/m
v = ?F/?
v = ?300/0,05
v = ?6000
v = 77 m/s
EXPLICAÇÃO:
Na física, dizemos que a onda se origina em meios elásticos como nas cordas, na superfície da água etc. Sendo assim, definimos uma onda como sendo um movimento oscilatório que se propaga num meio; sendo que nesses movimentos apenas a energia é transferida, isto é, não há transporte de matéria.
Sabemos que existem dois tipos de ondas e elas são classificadas como ondas mecânicas e ondas eletromagnéticas. Distinguimos uma onda mecânica de uma onda eletromagnética basicamente da seguinte forma:
- onda mecânica resulta de deformações provocadas em meios materiais, isto é, uma onda mecânica necessita de um meio material para se propagar.
- onda eletromagnética é o resultado da vibração de cargas elétricas, isto é, onda eletromagnética não necessita de um meio material para se propagar. Portanto, uma onda eletromagnética se propaga no vácuo.
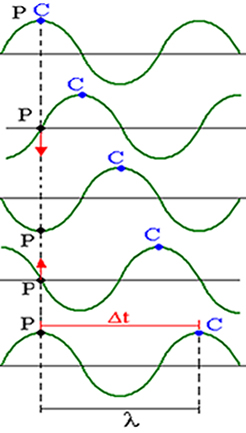
Para a propagação de uma onda, podemos usar o mesmo conceito para o cálculo da velocidade média:
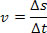
Podemos deduzir a velocidade com que uma onda se propaga; para isso basta fazermos o quociente entre o espaço em que a onda percorre em função do tempo. Analisemos a figura acima, onde temos a propagação de uma onda. Nela podemos ver que enquanto o ponto C percorre um comprimento de onda, cada ponto da corda executa uma oscilação por completo.
Por esse motivo é que podemos dizer que o tempo gasto para percorrer um comprimento de onda é o próprio período T da onda. Desta forma, tomando como base a expressão acima, enquanto o ponto C percorre uma distância ?s = ?, o tempo gasto é ?t = T. Desta forma, a velocidade de propagação de uma onda é dada por:
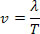
Ou podemos escrever da seguinte forma, como T = 1/f, temos:
v=? .f
Caso a fonte produtora da onda seja harmônica simples, o período e a frequência serão constantes. Assim, podemos dizer que a velocidade de propagação de uma onda numa corda é dada por:
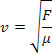
Na equação acima temos que:
- F é a tensão na corda
- ? é a densidade linear da corda
Vejamos o seguinte exemplo: Suponha que uma onda possui frequência de 8 Hz e esteja se propagando com velocidade igual a 200 m/s. Determine o comprimento de onda da onda.
Retirando os dados fornecidos pelo exercício, temos: f = 8 Hz e v = 200 m/s, aplicando a equação fundamental das ondas, temos:
v=? .f
200=? .8