Um carro descreve uma curva de 230m de raio. a) qu

Para resolver esses problemas, vamos usar as leis da física que governam o movimento circular uniforme.

a) Para encontrar o coeficiente de atrito entre os pneus e o asfalto, podemos usar a equação para a força centrípeta:

?

Onde:

• Fc? é a força centrípeta necessária para manter o carro na curva,
• $m$ é a massa do carro,
• $v$ é a velocidade do carro, e
• $r$ é o raio da curva.

A força centrípeta é fornecida pela força de atrito estático entre os pneus e o asfalto:

Onde:

• Fa? é a força de atrito,
• $?$ é o coeficiente de atrito entre os pneus e o asfalto, e
• $N$ é a força normal (o peso do carro, neste caso).

A força normal é igual ao peso do carro, $mg$, onde $g$ é a aceleração devido à gravidade.

Igualando as duas expressões para a força centrípeta, obtemos:

?

Cancelando $m$ de ambos os lados, temos:

?

Agora podemos resolver para $?$:

?

Substituindo os valores conhecidos:

Portanto, o coeficiente de atrito entre os pneus e o asfalto é aproximadamente 0.98.

Observe que neste caso, a constatação de que o atrito faz o papel de força centrípeta deve ser intuitiva. Se nos movemos em linha reta, a força de atrito estará sempre na mesma direção do movimento, mas com sentido contrário, porque ela sempre o atrapalha, nunca o facilita. Quando uma objeto se move em círculos, a força centrífuga, que nada mais é do que uma abstração da lei de inércia, empurra o objeto para fora do círculo. Enquanto o objeto tende a se mover lateralmente para fora, a força de atrito atrapalhará esse movimento, puxando ele de volta para dentro.

Na prática, a força de atrito é uma interação genuína entre dois corpos e sua natureza é eletromagnética. Toda vez que dois objetos entram em contato, suas cargas opostas se atraem fortemente gerando essa sensação de "grude", mas que pode durar somente alguns milésimos de segundo. A força de atrito será tão maior quanto for a superfície de contato, de modo que mais cargas entram em contato e ficam mais próximas umas das outras.

Apesar de não ser uma força real, a força centrífuga descreve um efeito bastante prático no movimento circular uniforme. Como o movimento é dito uniforme, a velocidade não muda, apenas a direção. E a direção muda de forma constante, porque existe um equilíbrio dinâmico entre a força centrífuga e a força centrípeta. Em termos mais realistas, toda a tendência de "escapar" do círculo precisa ser anulada pela força centrípeta. A força centrífuga surge então como uma analogia ao movimento retilíneo, onde um objeto se move de maneira constante tanto em magnitude como em direção, porque é puxado para os lados por duas forças de mesma intensidade. 

b) Agora, para determinar o ângulo de inclinação lateral da curva, podemos usar a mesma equação para a força centrípeta, considerando que a força peso é perpendicular à força centrípeta, e que a pista e a horizontal formam um triângulo retângulo semelhante ao triângulo formado pelas forças no diagrama de corpo livre do carro (tente visualizar isso girando as forças 90° no sentido anti-horário).

 

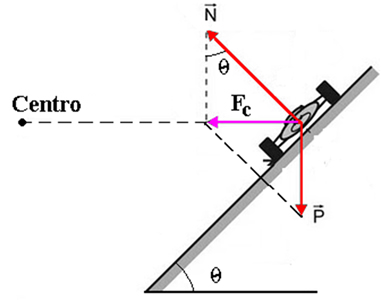
Portanto, podemos igualar as duas expressões para a força centrípeta:

?

Cancelando $m$ de ambos os lados, temos:

?

Agora, isolamos $?$:

?

Primeiro, convertemos a velocidade para m/s:

90?km/h=90×1000/3600?m/s=25?m/s

Agora, substituímos:

Portanto, o ângulo de inclinação lateral da curva para que o carro descreva a mesma com uma velocidade máxima de $90\text{km/h}$ é aproximadamente 15.50°.

Se você estiver em uma pista sobrelevada e quiser fazer a ultrapassagem de outro veículo pelo lado de fora da curva, basta apenas acelerar o veículo, sem girar o volante. Mas se você quiser aumentar a velocidade e permanecer no mesmo nível horizontal, basta que, simultaneamente, você aumente a velocidade do veículo e gire o volante do carro para dentro da curva. Agindo dessa maneira, o uso da força de atrito impedirá que o carro se dirija para fora da curva.

A fim de simplificar o que foi mencionado podemos fazer uma experiência bastante simples. Se pegarmos um funil e colocarmos uma bolinha de gude dentro e começarmos a fazer com que ela gire, perceberemos que ela descreverá uma curva horizontal. Agora se aumentarmos a velocidade da bolinha de gude veremos que ela tende a “subir” para a lateral do funil. Caso a velocidade da bolinha diminua, ela tende a “cair” para o centro do funil. Isso acontece porque, na equação que representa esse movimento, tanto a massa como a inclinação são constantes, de modo que qualquer variação na velocidade, isto é, aceleração, precisa ser compensada por uma variação no raio da curva descrita, de modo que o sistema retorne ao equilíbrio dinâmico. 

Para resolver esse problema, podemos usar as leis de Newton para movimento circular. a) Para determinar o coeficiente de atrito entre os pneus e o asfalto, podemos usar a seguinte equação: \[ v_{\text{max}} = \sqrt{R \cdot g \cdot \mu} \] Onde: - \( v_{\text{max}} = 47 \) m/s (velocidade máxima), - \( R = 230 \) m (raio da curva), - \( g = 9,81 \) m/s² (aceleração devido à gravidade), - \( \mu \) é o coeficiente de atrito que queremos encontrar. Substituindo os valores na equação: \[ 47 = \sqrt{230 \cdot 9,81 \cdot \mu} \] \[ 47 = \sqrt{2256,3 \cdot \mu} \] \[ 47^2 = 2256,3 \cdot \mu \] \[ \mu = \frac{47^2}{2256,3} \] \[ \mu \approx \frac{2209}{2256,3} \] \[ \mu \approx 0,978 \] Portanto, o coeficiente de atrito entre os pneus e o asfalto é aproximadamente 0,978. b) Para determinar o ângulo de inclinação lateral da curva, podemos usar a seguinte equação: \[ \tan(\theta) = \frac{v_{\text{max}}^2}{R \cdot g} \] Onde: - \( \theta \) é o ângulo de inclinação lateral, - \( v_{\text{max}} = 90 \) km/h = \( \frac{90 \times 1000}{3600} \) m/s = 25 m/s (velocidade máxima), - \( R = 230 \) m (raio da curva), - \( g = 9,81 \) m/s² (aceleração devido à gravidade). Substituindo os valores na equação: \[ \tan(\theta) = \frac{25^2}{230 \cdot 9,81} \] \[ \tan(\theta) = \frac{625}{2256,3} \] \[ \theta = \arctan\left(\frac{625}{2256,3}\right) \] \[ \theta \approx \arctan(0,277) \] \[ \theta \approx 15,6° \] Portanto, o ângulo de inclinação lateral da curva deve ser de aproximadamente 15,6 graus para que o carro descreva a mesma com uma velocidade máxima de 90 km/h.