A minha dúvida é de como eu posso chegar em um resultado em pi sendo que não deu nenhum valor em pi na questão e tambem como eu posso achar ele.
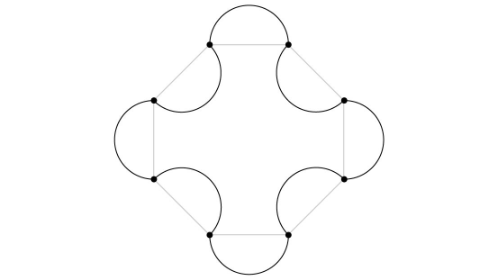
Com base em um octógono regular cujo lado mede 3 cm, constrói-se uma logomarca substituindo-se cada lado do polígono por uma semicircunferência, conforme a figura.
O perímetro dessa logomarca, em cm, é igual a
A) 12pi
B) 18pi
C) 24pi
D) 36pi
E) 48pi
Olá Davi. Tudo bem?
Não se preocupe com o pi. Ele vai aparecer no meio da questão :)
Vamos lá.
A primeira coisa que vc tem que reparar é que a logomarca é feita de várias semicircunferências (metade de uma circunferência), como diz a questão.
Algumas dessas semicircunferências aparecem viradas pra dentro e outras aparecem viradas pra fora.
Se vc reparar no desenho, cada lado do octógono está ligando uma semicircunferência do início ao final dela. Como se fosse a letra D, onde a semicircunferência é a parte curva e o lado do octógono é a parte reta.
Desta forma, o lado do octógono é o diâmetro da circunfrência que formou esta semicircunferência.
Só imaginar que pegamos uma circunferência e cortamos ela exatamente no meio. Daí descartamos uma metade e ficamos como a nossa letra D.
O perímetro de uma cincunferência é calculado na seguinte expressão:
P=2*pi*r
onde,
Porém, nós queremos o perímetro da semicircunferência, que é metade do perímetro da circunferência inteira.
Podemos calcular então da seguinte forma:
P=(2*pi*r)/2
P=pi*r
Para descobrir o valor do perímetro da circunferência precisamos saber o raio dela.
O raio de uma circunferência sempre vale metade do valor do seu diâmetro.
Como já vimos, o valor deste diâmetro é o valor do lado do octógono, que a questão diz que é 3cm.
Logo o raio vale metade disso: 1,5cm.
Voltando a expressão:
P=pi*r
Substituindo o valor do raio, temos:
P=pi*1,5
P=1,5*pi (apenas inverti a ordem)
Pronto.
Achamos o valor do perímetro de uma das semicircunferências de um dos lados do octógono.
Nós temos 8 semicircunferências idênticas que formam a logomarca.
Então, é só multiplicar isso por 8.
1,5*pi*8 = 1,5*8*pi = 12*pi
Letra A.
Espero ter ajudado :)


Boa noite, Davi. Tudo bem?
Alternativa A
O comprimento de uma circunferência calculamos da seguinte maneira: C = 2.pi.R
Na figura temos 8 meias circunferência que equivalem a 4 circunferencias, portanto:
Perímetro = 4.2.pi.1,5 = 12pi cm

Davi,
Repare que cada lado do octógono virou meia circunferência cujo diâmetro é o lado 3cm, logo cada uma tem raio igual a 1,5 (diâmetro = 2 x raio).
Se tomar cada metade da circunferência e juntar, você poderá ver que o perímetro da figura será exatamento do tamanho de 4 circunferências inteiras.
O tamanho da circunferência, ou seu contorno, ou seu perímetro é dado por 2 x pi x raio (repare qu o pi faz parte da fórmula, por isso ele não foi citado no enunciado do problemas)
logo o perímetro será:
4 . 2 . pi . 1,5
12 . pi
A) 12pi
Espero ter ajudado.
Fica com Deus!
