Diversas aplicações fazem uso das transformações lineares. Por exemplo, podemos utilizar essas aplicações para auxiliar no processamento de imagens e na criptografia.
Muitas vezes, nessas aplicações, precisamos identificar se a transformação linear é injetora. Para este fim, podemos trabalhar com o núcleo. O núcleo de uma transformação linear é dado por:
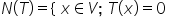onde 
representa o elemento nulo de
Dizemos que uma transformação linear é injetora se 
ou seja, o elemento nulo de 
é o único elemento pertencente ao núcleo de 
Outras vezes, necessitamos identificar o conjunto imagem da transformação linear 
que é dada pelo conjunto:
para algum 
Considere a transformação linear 
dada por 
é injetora?
existe 
tal que 
Deixe registrado todos os cálculos necessários para obter as respostas
Olá, Rael!
Para encontrar o núcleo de uma transformação linear, você deve igualar a expressão da transformação linear ao vetor nulo do espaço:
Fazendo a segunda equação menos a primeira, resulta que 3y=0, de onde vem que y=0. Daí, substituindo em qualquer uma das duas equações, resulta que x=0. Logo, o Núcleo é formado apenas pelo vetor nulo, portanto T é injetora.
Para responder ao item 2, você tem que fazer algo parecido: resolver o sistema
Proceda de forma análoga: faça a segunda equação menos a primeira, de onde você obtém e, substituindo y na segunda equação, vem que
.
Espero ter te ajudado. Atenciosamente, Professor Josafá!
Olá, Rael. Tudo bem? O ambiente de dúvidas não é o mais adequado para escrever soluções detalhadas, mas vamos tentar te ajudar.
1. Suponha que satisfazem
Então,
Deste modo, Por outro lado, também temos
Portanto, devemos ter . Mas isto só ocorre se
Logo, a função T é injetiva.
Para falarmos com mais detalhes sobre a sobrejetividade, por favor, considere contratar uma aula. Bons estudos!
a) Para verificar que T é injetora existem duas formas de fazer isso.
1ª forma: usando a definição.
Uma função é injetora se para quaisquer
em
tivermos
ou, de modo equivalente, se
. Para a função
temos para
e
que
Dessas equações obtemos
logo
.
Porém esta igualdade só tem sentido se pois do contrário teremos, após cancelar
dos dois membros, a igualdade -1=2, um absurdo! Portanto
. Substituindo nas igualdades acima encontramos que
. Portanto T é injetora.
2ª forma: mostrando que .
Existe um resultado da álgebra linear que afirma que uma transformação linear é injteora se, e somente se, o seu núcleo é zero. Então basta igualar e mostrar que
e
. Então
Substraindo as equações obteremos e substituindo na segunda obtemos
. Portanto T é injetora.
b) Também existem duas formas de resolver.
1ª forma: Usando a definição.
Dados a e b, queremos encontrar x e y tais que . Basta substituir direto:
Resolvendo encontramos
2ª forma: usando o teorema do núcleo-imagem
Se é uma transformação linear entre espaços vetoriais de dimensão finita, então a dimensão do núcleo mais a dimensão da imagem é igual a dimensão do domínio, isto é,
Como já provamos que e como
, a dimensão do domínio é 2, logo a igualdade acima dá que a dimensão da imagem de T é 2, que é igual a dimensão do contra-domínio, logo
, isto é, T é sobrejetora, portanto para qualquer
, existe
tal que
.
Aulas particulares
