Marque falso ou verdadeiro nas alternativas a seguir e justifique.
a) Sejam = (1,2,3) ,
= ( -3,2,1) e
= (-1,2,0) (dados na base canônica) . Então existe ao menos uma base B de R³ na qual as coordenadas de
,
,
são, respectivamente, (1,0,0) ; (0,1,0) e (0,0,1).
b) Se B é um espaço vetorial de dimensão 2 sobre R e B = { ,
} é uma base de V. Seja
=
α1 + α2
, então α1 e α2 são coordenadas de
em relação a base B de V.
c)
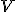, fixada uma base 
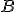, dois vetores que tenham as mesmas coordenadas na base 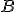são necessariamente iguais. d) Seja B = {,
} uma base de um espaço vetorial V. Sejam (a1 , b1) e (a2 , b2) as coordenadas dos vetores
e
(respectivamente) na base B. Se A =
e det(A) diferente de zero, então o conjunto S = {
,
} é linearmente independente.
e)
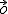é o vetor nulo de um espaço vetorial 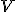então suas coordenadas serão todas iguais a zero independentemente da escolha da base fixada.f) Seja B = {, }
uma base de um espaço vetorial V. Se
= α1
- α2
e
=
β1 - β2
então α1 = β1 e α2 = β2
Alguém poderia me dar pelo menos uma direção em cada uma das alternativas ?
Nessa sessão respondemos a dúvidas pontuais.
Aulas particulares
