Como pudemos perceber em nossos estudos, os conceitos de limite e continuidade para funções de duas e três variáveis são uma extensão dos conceitos de limite e continuidade para funções de uma variável, já estudados. Avalie se a função  definida por
definida por  se
se  e
e  é contínua em
é contínua em 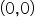
Não se esqueça de exibir todos os cálculos realizados.
Olá Rael,
Como você disse, o conceito de continuidade de uma função de duas variáveis é uma extensão do conceito de continuidade para valores reais. Assim, para que uma função definida em seja contínua num ponto
, deve satisfazer
. Note que, no caso da função do enunciado, pede-se para analisar continudade em
. Pois bem, lembre-se que agora o domínio de
é o plano
assim a idéia de "se aproximar de
" não é mais uma aproximação apenas por um eixo (como era para funções definidas em valores reais) mas agora podemos nos aproximar do ponto por qualquer direção.
Vou tomar duas direções distintas: primeiro vamos nos aproximar da origem pela reta , depois pela reta
, observe que se aproximar da origem por essas duas retas é o mesmo que fazer
. Vamos ver o que acontece:
Pela rela :
Pela reta :
Ou seja, notemos que se aproximando da origem por caminhos distintos, obtemos valores distintos para o limite, o que não deveria ocorrer se a função fosse contínua (para estabelecer uma analogia com funções reais, pense que isso é como se os limites laterais fossem distintos). Logo, concluímos que não é contínua em
.
Outra forma de ver isso (deixo para você pensar) é por coordenadas polares, tome e faça
, se o resultado final depender de
, então a função não é contínua na origem. (OBS. Usar coordenadas polares só funciona quando analisamos o limite na origem, além disso, mesmo que calculando esse limite vc encontre algo que não dependa de
isso não significa que a função é contínua no ponto, só temos a validade da contrapositiva: se o limite depende de
, a função não é contínua).
Espero ter ajudado!
Qualquer dúvida pode entrar em contato:
email: pedro.bortolucci@gmail.com
whatsapp: (19) 97112-2019
