Situação real: vou comprar 100 cestas básicas medindo cada uma 19 cm de altura, 35 cm de largura e 38 cm de comprimento. O caminhão que vai transportá-las mede 2,10 m de largura, 2,30 m de altura e 4,5 m de comprimento. As cestas caberão neste caminhão?
Considerando as informações dadas, temos:
Capacidade do caminhão: 2,3x4,5x2,1=21,73m^3.
Capacidade da cesta básica: 0,19x0,35x0,38=0,02527m^3.
Quantidade de cesta básica que cabem no caminhão: 21,73/0,02=~1.086,5.
Logo, caberá as 100 cestas básicas.

Primeiro, vamos converter todas as medidas para a mesma unidade (metros):
Medidas das cestas básicas:
O volume total das cestas (2,527 m³) é muito menor que o volume do caminhão (21,735 m³), então em termos de volume, as cestas cabem no caminhão.
Precisamos també verificar o arranjo das cestas dentro do caminhão para garantir que elas realmente caibam fisicamente. Considerando a melhor forma de empilhá-las:
Cestas na largura:
Cestas na altura:
Cestas no comprimento:
Portanto, o caminhão tem capacidade suficiente para transportar as 100 cestas básicas tanto em termos de volume quanto em termos de arranjo físico.
Qualquer dúvida sobre a resolução estou disponível para detalhes

Volume de 1 cesta = 19cm x 35 cm x 38cm =
Volume de 100 cestas = 100 x 25270 = =
Volume da caçamba do caminhão = 2,1m x 2,3m x 4,5m =
As cestas cabem no caminhão, pois
volume da caçamba >> volume de 100 cestas


Oi, Carlos, tudo bem?
Então, trabalhar com volumes de sólidos como cubo e paralelepípedo é muito simples, basta multiplicar o comprimento com a largura e a altura. O seu problema, na verdade, se chama CONVERSÃO: não se pode comprar volumes de duas figuras idênticas sem colocar elas na mesma unidade.
Você nos forneceu dois sólidos em unidades diferentes para saber que quantidade de cestas básicas caberiam num caminhão baú, é isso mesmo? Primeira coisa para se resolver um problema assim é definir em qual unidade de comprimento você vai fazer seu cálculo...ou por outro lado pode também resolver nas unidades respectivas mas teria que escolher qual unidade para fazer a comparação final.
Comigo, resolvi fazer todos em centímetros. Assim fica mais simples de lidar com a comparação no final. Dessa forma pude depois fazer o cálculo dos dois volumes:
V1: Volume da Cesta Básica
V2: Volume do baú do caminhão.
Este valor é de APENAS 1 cesta básica. Para saber quanto seriam 100 cestas, basta multiplicar por 100.
Lembrando que eu, Élida, escolhi converter a unidade "metros" para a unidade " centímetros". O resultado fica:
Como analisar estes dois resultados?
Você pode ver de duas formas:
1. OU você divide o V2 pelo V1, pra saber qual seria a quantidade máxima de cestas básicas que o caminhão poderia suportar;
2. OU multiplica o volume da cesta por 100 ( que é a quantidade de cestas básicas que você quer comprar) e compare se essa quantidade é maior ou menor que o volume do caminhão.
Vou começar com o tópico 2. Por ser a forma mais simples de resolver este problema.
Você viu que o seu V1 deu 25.270cm³. E você tinha dito que quer comprar 100 destas com este volume. Então:
Ou seja, o volume total da sua cesta básica é de 2.527.000cm³. Se a gente compara esse valor com o volume do caminhão?
Ou seja, vai ter espaço de sobra no baú do caminhão.
Agora, vamos analisar o tópico 1? Também é simples, mas precisa calcular.
O Tópico 1 sugere a seguinte divisão:
Qual é a idéia aqui? É saber a capacidade máxima que o baú do caminhão suporta para levar as cestas básicas. Por isso aqui também existe a necessidade dos volumes estarem na mesma unidade de medida. Temos:
Ou seja, o baú do caminhão comporta um pouco mais de 800 cestas básicas . Isso é quase 8 vezes a quantidade que você quer comprar .
Então, fique bem tranquilo que as suas cestas básicas caberão no caminhão. Certinho? Vai dar certo!

Basta calcular o volume do caminhão e o volume da caixas, caso o volume do caminhão for maior que o das caixas, caberá.
Volume caminhão = 2,30 x 4,5 x 2,1 = 21,735 m³
Volume caixa = 0,19 x 0,35 x 0,38 = 0,02527 m³
Para saber o volume de 100 caixas basta multiplicar por 100 que seria 2,527 m³
Sendo assim, as caixas com certeza caberão no caminhão já que o volume do caminhão é bem superior ao volume das caixas.

Bom dia Carlos. Vamos que vamos:
Ver a planilha abaixo.
| Dados: | ||
| Dados de cada caixa | ||
| Altura | 19 | cm |
| Altura (a) | 0,19 | m |
| Largura | 35 | cm |
| Largura (b) | 0,35 | m |
| Comprimento | 38 | cm |
| Comprimento © | 0,38 | m |
| Dados do caminhão | ||
| Largura (d) | 2,1 | m |
| Altura (e) | 2,3 | m |
| Comprimento (f) | 4,5 | m |
| Cálculos: | ||
| Volume da cada caixa | 0,02527 | m3 |
| (V=a*b*c) | ||
| Volume da carroceria do caminhão (=d*e*f) |
21,735 | m3 |
| Número da caixas (#) = Vcaminhão/V caixa |
860,1108 | # |
Logo, a carroceria do caminhão poderá acomodar as suas 100 caixas de cestas básicas com facilidade.
Sucesso!!!!

Volume de uma cesta básica:
Volume de uma cesta básica:
Vcesta=Altura×Largura×Comprimento=0,19×0,35×0,38 m3V_{cesta} = \text{Altura} \times \text{Largura} \times \text{Comprimento} = 0,19 \times 0,35 \times 0,38 \text{ m}^3 Vcesta=0,02453 m3V_{cesta} = 0,02453 \text{ m}^3Volume total das 100 cestas básicas:
Vtotal=100×Vcesta=100×0,02453 m3V_{total} = 100 \times V_{cesta} = 100 \times 0,02453 \text{ m}^3 Vtotal=2,453 m3V_{total} = 2,453 \text{ m}^3Espaço disponível no caminhão:
Volume disponível no caminhão:
Vcaminhao=Altura×Largura×Comprimento=2,30×2,10×4,5 m3V_{caminhao} = \text{Altura} \times \text{Largura} \times \text{Comprimento} = 2,30 \times 2,10 \times 4,5 \text{ m}^3 Vcaminhao=21,945 m3V_{caminhao} = 21,945 \text{ m}^3Verificação se as cestas cabem no caminhão: O volume total das cestas é 2,453 m32,453 \text{ m}^3.
Como 2,453 m3<21,945 m32,453 \text{ m}^3 < 21,945 \text{ m}^3, podemos concluir que as 100 cestas básicas cabem no caminhão. O espaço disponível no caminhão é mais do que suficiente para acomodar todas as cestas.
Portanto, sim, as 100 cestas básicas caberão no caminhão que tem as dimensões especificadas

Para determinar se as 100 cestas básicas caberão no caminhão, precisamos calcular os volumes e verificar se há espaço suficiente, considerando também a organização das cestas no caminhão.
Primeiro, vamos converter todas as medidas para a mesma unidade (metros).
As dimensões de cada cesta básica em metros são:
O volume de uma cesta básica é:
Agora, o volume total das 100 cestas:
As dimensões do caminhão são:
O volume do caminhão é:
Agora que sabemos que o volume total das cestas é menor que o volume do caminhão, precisamos verificar se as cestas podem ser organizadas dentro do caminhão, respeitando suas dimensões.
Vamos considerar as cestas organizadas em diferentes orientações para ver se cabem dentro do caminhão.
Cestas dispostas com a base de 35 cm x 38 cm e altura de 19 cm.
Número de cestas ao longo da largura do caminhão:Número de cestas ao longo do comprimento do caminhão
Número de cestas ao longo da altura do caminhão:
Número total de cestas nessa orientação:
Cestas dispostas com a base de 19 cm x 38 cm e altura de 35 cm.
Número de cestas ao longo da largura do caminhão:
Número de cestas ao longo do comprimento do caminhão:
Número de cestas ao longo da altura do caminhão:
Número total de cestas nessa orientação:
Cestas dispostas com a base de 19 cm x 35 cm e altura de 38 cm.
Número de cestas ao longo da largura do caminhão:
Número de cestas ao longo do comprimento do caminhão:
Número de cestas ao longo da altura do caminhão:
Número total de cestas nessa orientação:
Em todas as orientações, o número de cestas que cabem no caminhão é maior do que 100. Portanto, as 100 cestas básicas caberão no caminhão sem problemas.

Situação real: vou comprar 100 cestas básicas medindo cada uma 19 cm de altura, 35 cm de largura e 38 cm de comprimento. O caminhão que vai transportá-las mede 2,10 m de largura, 2,30 m de altura e 4,5 m de comprimento. As cestas caberão neste caminhão?
Para saber se as cestas caberão neste caminhão, vamos calcular o volume V do caminhão, o volume v de cada cesta.
Logo após, vamos multiplicar 100 por v, 100v.
Para concluir devemos verificar se V é maior ou igual a100v
Lembrando que volume é: v = a.b.c, onde a é altura, b é a largura e c é o comprimento do sólido.

Boa noite Carlos, tudo bem?
Na tabela abaixo você encontrará o cálculo de volume das 100 cestas básicas e também do caminhão. Basta se atentar para a conversão para a mesma unidade de medida (metros) e também a fórmula que calcula o volume, neste caso, supondo o formato de paralelepípedo para os objetos.
Como o volume que será ocupado pelas 100 cestas (2,527 m3) é inferior ao volume disponível no caminhão (21,735 m3) a resposta para a pergunta no enunciado é: SIM, as cestas caberão no caminhão.
| Objeto | Altura(m) | Largura(m) | Comprimento(m) | Volume (m3) = Altura * Largura * Comprimento |
| Cesta | 19cm=0,19m | 35cm = 0,35m | 38cm=0,38m | 0,19*0,35*0,38 = 0,02527 m3 como são 100 então 2,527 m3 |
| Caminhão | 2,3m | 2,10m | 4,5m | 2,3*2,1*4,5 = 21,735 m3 |
Se tiver outras dúvidas, estou à disposição !
Abraços e bons estudos.

O caminhão e a cesta básica possuem formatos de paralelepipedo. Logo, o volume é calculado pela seguinte fórmula:
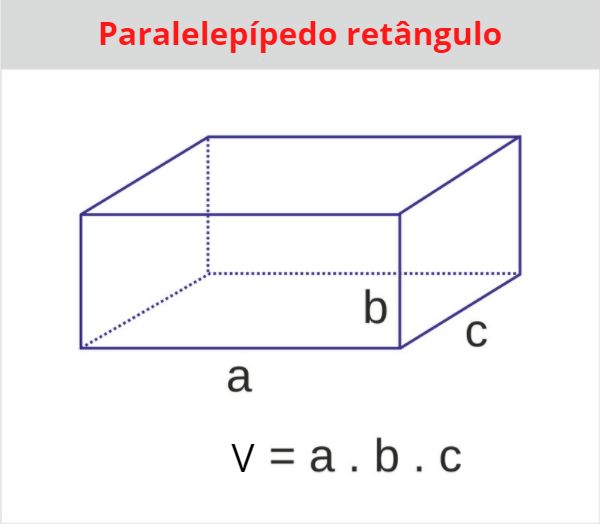
Volume do caminhão:
2,3x4,5x2,1=21,73 metros cúbidos
Volume da cesta básica:
0,19x0,35x0,38=0,02527 metros cúbidos
Neste sentido, a quantidade de cesta básica que cabem no caminhão é obtida por meio da razão (divisão) entre os volumes.
21,73/0,02
Como resultado, temos aproximadamente 1.086,5.
Como não é possível termos meia cesta básica no caminhão, dizemos que nele cabem 1.086 cestas básicas.
