A fórmula de Bhaskara é uma técnica utilizada para resolver equações quadráticas da forma:
[ ax^2 + bx + c = 0 ]
onde ( a ), ( b ) e ( c ) são coeficientes reais. A fórmula é dada por:
[ x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a} ]
Aqui, o discriminante (( \Delta )) é dado por:
[ \Delta = b^2 - 4ac ]
A partir do valor de ( \Delta ), podemos determinar a natureza das raízes da equação: - Se ( \Delta > 0 ), existem duas raízes reais e diferentes. - Se ( \Delta = 0 ), existe uma raiz real dupla. - Se ( \Delta < 0 ), as raízes são complexas.
Vamos aplicar a fórmula de Bhaskara à equação ( x^2 - x + 1 = 0 ).
Identificamos os coeficientes: - ( a = 1 ) - ( b = -1 ) - ( c = 1 )
Calculamos o discriminante:
[ \Delta = b^2 - 4ac = (-1)^2 - 4 \cdot 1 \cdot 1 = 1 - 4 = -3 ]
Como ( \Delta < 0 ), sabemos que a equação não possui raízes reais, e sim duas raízes complexas.
Agora, vamos usar a fórmula de Bhaskara para encontrar as raízes complexas:
[ x = \frac{{-(-1) \pm \sqrt{{-3}}}}{2 \cdot 1} = \frac{{1 \pm \sqrt{{-3}}}}{2} ]
Podemos reescrever ( \sqrt{{-3}} ) como ( i\sqrt{3} ) (onde ( i ) é a unidade imaginária).
Portanto, as raízes são:
[ x = \frac{1 \pm i\sqrt{3}}{2} ]
Assim, as duas raízes da equação ( x^2 - x + 1 = 0 ) são:
[ x_1 = \frac{1 + i\sqrt{3}}{2} \quad \text{e} \quad x_2 = \frac{1 - i\sqrt{3}}{2} ]


A Fórmula Sridharacharya é uma fórmula matemática usada para resolver equações quadráticas. A fórmula Sridharacharya também é comumente conhecida como fórmula quadrática. Sridharacharya forneceu um método para resolver as equações quadráticas e, portanto, recebeu o nome do grande matemático e é chamado de Fórmula Sridharacharya.
Esta formula so eh conhecida como Baskara no Brasil, no resto do mundo e principalmente na Europa eh conhecida como formula de VIETE. A partir de VIETE, FERMAT E DESCARTES, foram desenvolvidas formulas matematicas mais avancadas como as EQUACOES CUBICAS E BIQUADRATICAS, as primeiras CUBICAS, estudas por FERRARI e BOMBELLI , as BIQUADRATICAS estudos por EVARISTA GALOUIS. Galouis com isso desenvolveu a ALGEBRA ABSTRATA, infelizmente morreu por um desfeto passional em uma batalha. Galouis eh considerado o maior genio da matematica e teriamos muitas revolucoes sem sua morte prematura ao 21 anos, a Algebra Abstrata se inserir em muitos campos da ciencia moderna e contemporanea.
Resume-se em resolucoes de raizes,, a partir da equacao quintupla nao existem solucoes viaveis, recorre-se a metodos anteriores , como quadraticas , cubicas e biqaudratica ou quarto grau...
att.
OUTRO MÉTODO:
O método da soma e produto é um método prático utilizado para determinar as raízes das equações do 2º grau. Ele é conhecido desta forma, porque faz uso de duas importantes relações de soma e produto entre as raízes e os coeficientes a, b e c da equação do segundo grau.
É claro que por envolver o nosso raciocínio e não entregar os resultados de uma forma direta como acontece na fórmula de Bhaskara, por exemplo, esse método pode não ser tão simples no início de nossa jornada rumo ao conhecimento. Assim, para facilitar a utilização do método, vocês podem seguir os passos descritos abaixo.
x²-x+1=0 ax²-bx+c=0
a=1 b=-1 c=1
=1
=1
3. QUANDO O MÉTODO DA SOMA E PRODUTO NÃO É O MAIS APROPRIADO
Como comentamos no início do texto, o método da soma e produto pode facilitar e agilizar muito a obtenção das raízes de uma equação do 2º grau, principalmente quando estas são números inteiros. Contudo, quando as raízes são fracionárias ou complexas, fica difícil ou até mesmo impossível defini-las através deste método.
3.1 Quando pelo menos uma das raízes é uma fração ou um número decimal

Para entendermos direitinho quando o método da soma e produto não é o mais indicado, vamos tentar seguir os passos apresentados anteriormente para encontrar as raízes da equação 2x2 + 3x – 5 = 0. Vejam só o que irá acontecer!
Dada a equação 2x2 + 3x – 5 = 0, sabemos que a = 2, b = 3 e c = – 5. Portanto, o quociente – b/a é igual a – 3/2 e o quociente c/a é igual a – 5/2. Assim, chegamos as seguintes relações:
x1 + x2 = – 3/2
x1 ? x2 = – 5/2.
E aí, pessoal, quais são os números reais que somados resultam em – 3/2 e que multiplicados resultam em – 5/2? Quem já praticou muito o método da soma e produto ou tem facilidade com a soma e a multiplicação de frações, vai identificar que as raízes x1 e x2 que procuramos valem 1 e – 5/2. Mas, para muitos alunos, esses resultados podem não ser tão claros, principalmente de forma rápida.
3.2 Quando as raízes da equação do 2º grau são números complexos

Dada a equação – x2 + 2x – 2 = 0, sabemos que a = – 1, b = 2 e c = – 2. Portanto, o quociente – b/a é igual a 2 e o quociente c/a também é igual a 2. Assim, chegamos as seguintes relações:
x1 + x2 = 2
x1 ? x2 = 2.
E agora, vocês sabem dizer quais são os dois números reais que somados e multiplicados resultam em 2? Um tanto estranho, não é mesmo? A verdade, pessoal, é que as raízes desta equação não são números reais, mas sim, números complexos, um assunto no qual não nos aprofundaremos aqui. Por isso, não ficou evidente nenhuma possibilidade real que pudesse satisfazer as duas relações ao mesmo tempo. Em forma de conjunto solução, podemos representar essa situação através de um conjunto vazio.
S = { }
Tendo esses exemplos em vista, pessoal, quando vocês resolvem usar o método da soma e produto, mas percebem que a solução para as relações de soma e produto não é tão óbvia, não hesitem em abandonar o método e utilizar logo a fórmula de Bhaskara! A partir do cálculo do discriminante da função quadrática (?), é possível saber se as raízes da equação são reais e iguais, reais e distintas ou mesmo complexas. O método da soma é produto é válido quando agiliza o cálculo das raízes, do contrário, o ideal é utilizar a fórmula de Bhaskara mesmo.
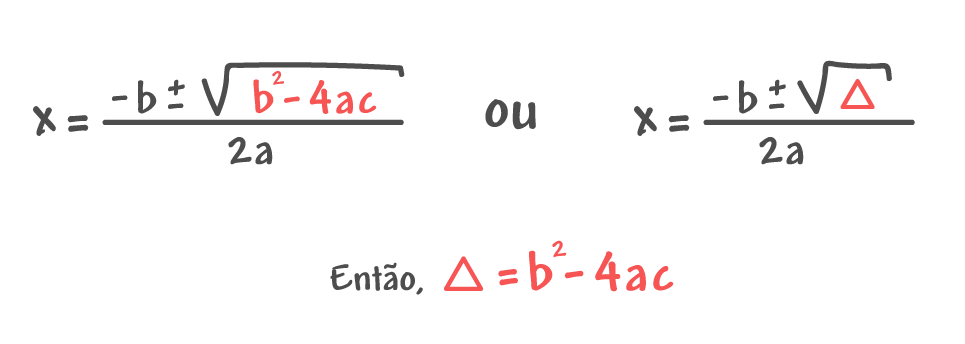
Você sabe como utilizar a fórmula de Bhaskara no cálculo das raízes de uma equação do 2º grau? Não? Então, clique aqui.
Entendido? No próximo item nós vamos resolver mais algumas equações do 2º grau através do método da soma e produto. Vem comigo!
