Uma progressão geométrica (PG) é uma sequência de números em que cada termo após o primeiro é obtido multiplicando o termo anterior por uma constante chamada de razão (r).
A fórmula geral para o enésimo termo (n-ésimo) de uma PG pode ser expressa como:
Onde: - é o n-ésimo termo da PG, - é o primeiro termo, - é a razão da PG, - é a posição do termo na sequência.
Exemplo: Se temos uma PG onde o primeiro termo é 2 e a razão é 3, a sequência seria: - 1º termo: - 2º termo: - 3º termo: - 4º termo:
Portanto, a sequência seria 2, 6, 18, 54, e assim por diante.
As PGs podem ser finitas ou infinitas e podem envolver números negativos, fracionários e até mesmo decimais, dependendo dos valores utilizados.
Progressões geométricas foram encontradas em tábuas babilônicas que datam de 2100 a.C. Progressões aritméticas foram encontradas pela primeira vez no Papiro Ahmes, que é datado de 1550 a.C. Os nomes para essas noções, no entanto, parecem ter levado consideravelmente mais tempo. Em alguns casos, não havia um padrão para como se referir a elas (mesmo o termo progressão não era necessariamente um padrão).
O mais próximo que posso chegar do raciocínio por trás dos nomes é que cada termo em uma sequência geométrica (aritmética) é a média geométrica (aritmética) de seu sucessor e predecessor. A lógica por trás dos nomes dessas médias é um pouco mais clara: se vemos as quantidades A e B como os comprimentos dos lados de um retângulo, então a média geométrica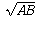 
é o comprimento dos lados de um quadrado tendo a mesma área que esse retângulo. Isso era visto naquela época como um problema muito geométrico : encontrar as dimensões de um quadrado tendo a mesma área que uma determinada figura (nesse caso, retângulo).
Embora a média aritmética ( A + B )/2 também possa ser interpretada geometricamente (é o comprimento dos lados de um quadrado que tem o mesmo perímetro do retângulo), os comprimentos eram vistos mais como conceitos aritméticos (porque é fácil lidar com comprimentos por adição e subtração comuns, sem ter que pensar em conceitos bidimensionais, como área).
Ambos os conceitos envolvem aritmética. Também é verdade que ambos os conceitos podem ser interpretados geometricamente. No entanto, nos tempos antigos, um era visto muito mais geometricamente do que o outro, daí os nomes. Espero que os parágrafos acima esclareçam o porquê disso.
De forma prática, uma progressão geométrica (PG) é uma sequência de números em que cada termo, a partir do segundo, é obtido multiplicando o termo anterior por um valor constante, chamado razão da PG.
Aulas particulares
