A tangente é um conceito que aparece em várias áreas da matemática, principalmente na geometria e na trigonometria.
Definição Geométrica: Em um círculo, a tangente a uma circunferência em um ponto específico é uma linha reta que toca a circunferência apenas nesse ponto. Ou seja, ela não atravessa o círculo e apenas 'toque' na curva.
Definição Trigonométrica: Na trigonometria, a tangente de um ângulo é uma das funções trigonométricas básicas. Para um ângulo ? em um triângulo retângulo, a tangente é definida como a razão entre o comprimento do cateto oposto ao ângulo e o comprimento do cateto adjacente. Matematicamente, é expressa como:
[ \tan(?) = \frac{\text{cateto oposto}}{\text{cateto adjacente}} ]
Além disso, em termos da circunferência unitária, a tangente de um ângulo pode ser definida como a coordenada (y) da interseção do segmento de reta que representa a tangente (no ângulo) com a reta tangente à circunferência unitária.
Aplicações: A tangente é utilizada em várias aplicações, como:
Resolução de problemas em trigonometria, sendo fundamental na análise de triângulos.
Essas são algumas maneiras de entender o conceito de tangente na matemática! Se você tiver uma dúvida mais específica ou um exemplo concreto que gostaria de discutir, sinta-se à vontade para perguntar.
O problema da Tangente foi proposto por Isaac Barrow, isso culmina com o Calculo Diferencial e Integral Construindo Por Isaac Newton e Leibniz...
Método de Isaac Barrow
Este método foi apresentado no trabalho matemático de Barrow Lectiones opticae et geometricae. Ele utiliza uma abordagem muito próxima do processo moderno de diferenciação.
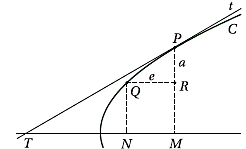
Para ilustrar o método, vamos novamente resolver o problema anterior: escrever a equação da reta tangente à curva y2 = 2x no ponto (8, 4).
Barrow resolvia esse problema calculando o valor da razão a/e em que a e e são catetos (paralelos aos eixos) do triângulo PQR.
Método de Pierre de Fermat
O método de Fermat para as tangentes foi apresentado em 1629 junto com o método para determinar máximos e mínimos de funções.
Método de René Descartes
Para escrever, por exemplo, a equação da reta tangente à curva y2 = 2x no ponto P(8, 4), a ideia de Descartes foi a de encontrar a equação de uma circunferência, de centro no eixo Ox, passando pelo ponto (8, 4) e tal que, nesse ponto, a parábola e a circunferência tivessem a mesma reta tangente. Isso porque na circunferência a reta normal a uma tangente passa pelo centro da circunferência, o que permite obter facilmente a equação da reta tangente a essa curva e, portanto, à parábola. Acompanhe os cálculos:
AQUI TEM TODA UMA BASICA EXPLICACAO
https://rpm.org.br/cdrpm/75/9.html
A tangente que da origem ao calculo diferencial e integral de Newton e Leibniz, teve influencia de Descartes e Pierre Fermart, lembrando que Os livros e Tratados por exemplo de Euclides , A exaustao de Eudoxo, Arquimedes , Antifona e VARIOS OUTROS PRE-SOCRATICOS E ESCOLAS GREGAS SOCRATICAS, O Olho de Horus com teoria infinetesimais de series , a Seita Pitagorica Matematica, e Euclides de Alexandria nos 12 elementos.
QUE TANGE , TRACE UMA RETA NO CENTRO DA CIRCUFERENCIA...
TRACE UMA RETA TANGENTE A LINHA DA CIRCURFERENCIA, FORMANDO 90 GRAUS...
QUANDO FORMA 90 GRAUS ESSA E A RETA TANGENTE..
PALAVRAS CHAVES...
RETA NORMAL
COEFICIENTE ANGULAR
A palavra tangente vem do latim tangens, que significa, tocando. Assim , uma tangente um curva e uma reta que toca a curva. Ou seja , uma reta tangente deve ter a emsma direcao e sentido que a curva no ponto de contato. Como tornar precisa essa ideia
Para um circulo poderiamos simpesmente seguir Euclides e dizer que a tangente e uma reta que intercepta o circulo uma unica vez, conforme a figura 1(a). PAra as curvas mais complicas essa definicao e inadequada. A Figura 1 b mostra duas retas, l e l, passando por um ponto P sobre uma curva C. A reta l intercepta C somente uma vez, mas certamente nao aaprenta o que pensamos ser uma reta tangente. A reta t , por outro lado, aparenta se uma tangente, mas intercepta C duas vezes.
Pagina 87 James Stweart https://tsxvpsbr.dyndns.org/arquivos/UFFS/James%20Stewart%20-%205%C2%AA%20Edi%C3%A7%C3%A3o%20-%20Vol.1.pdf
Culmina isso em toda a resolucao do CALCULO DIFERENCIAL POR LIMITES E TODO CALCULO INTEGRAL POR CALCULO DE AREAS..
