Triangulo escaleno - circunscrito

BM= BN=X AM=AP=8-X CP=CN=6-X AP+PC=12 8-X+6-X=12 2X=2 X=1

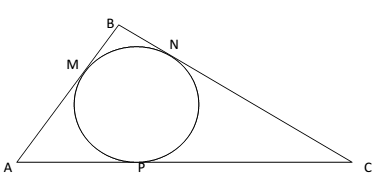
1º PASSO: Determinar o raio do circulo circunscrito (r) A = raiz(p.(p-AB).(p-BC).(p-AC)) - área do triângulo Eq. (1) p = (AB+BC+AC)/2 - semiperímetro de triângulo Eq. (2) Substituindo os valores em (2): p=(8+6+12)/2=13 Substituindo em (1): A = raiz(13.(13-8).(13-6).(13-12)) A = raiz(13.5.7.1) = raiz (455) = A = r.p Eq.(3) Logo, raiz(455)=r.13 r=1,6408 - raio do circulo circunscrito 2°PASSO: Determinar o ângulo (Cº) formado pelos segmentos de reta BC e AC Aplicando a lei dos cossenos: AB²=AC²+BC²-2.AC.BC.cos(C°) Eq. (4) Substituindo os valores em (4) 8²=12²+6²-2.12.6.cos (Cº) cos(Cº)=0,8056 C°=cos^-1(0,8056) C° = 36,3360 Chamando de O o ponto no centro do circulo circunscrito podemos considerar a semelhança de triângulos. O segmento BP forma um ângulo de 90º com o segmento AC e da mesma forma o segmento ON forma um ângulo de 90º com o segmento BC. Logo, temos que o triângulo formado pelos segmentos BC, PC e PB é semelhante ao triângulo formado OB, BN e NO. Assim, o ângulo formado pelos segmentos ON e OB é igual a C°=36,3360. 3º PASSO: Determinar o comprimento do segmento BN: tan (Cº)=BN/r Eq. (5) tan(36.3360) = BN/1,6408 BN = 1,2069