Para determinar a distância de um barco até a praia, um navegante utilizou o seguinte procedimento: a partir de um ponto A, mediu o ângulo visual α fazendo mira em um ponto fixo P da praia. Mantendo o barco no mesmo sentido, ele seguiu até um ponto B de modo que fosse possível ver o mesmo ponto P da praia, no entanto sob um ângulo visual 2 α. Suponha que o navegante tenha medido o ângulo α= 30° e, ao chegar ao ponto B, verificou que o barco havia percorrido a distância AB = 2 000 m. Com base nesses dados e mantendo a mesma trajetória, a menor distância do barco até o ponto fixo P será ?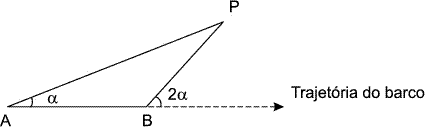
A resposta não deveria ser 2000 raiz de 3 ? ja que a trajetoria é horizontal somando o lado do triângulo retângulo e a base .
Como o ângulo no ponto B é 2α, o ângulo APB é α, o triângulo ABP é isósceles e portanto PB = AB = 2000 m.
Assim, a menor distância PC do barco até P será, observando-se o triângulo BPC, em que C é a projeção do ponto P sobre a reta que passa por AB, dada por
sen(2α) = PC/PB
PC = 2000 m * sen(60) = 2000 m * √3 / 2 = 1000 √3 m.


