Um cilindro circular reto está inscrito em um cone circular reto cujo raio da base mede 8 cm e cuja altura mede 16 cm. Sabendo que o raio da base do cilindro é metade do raio da base do cone, calcule o volume do cilindro.

Olá Vitória, tudo bem?
Para resolver esta questão é necessário visualizar o desenho:
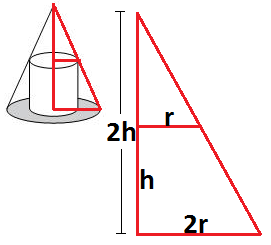
Dessa forma é possivel estabelecer uma fórmula de relação:
r / 2r = (2h-h) / 2h
Explicando a equação:
r = Parte de cima (horizontal)
2r = Parte de baixo (horizontal)
(2h - h) = Parte de cima (vertical)
2h = Parte inteira (vertical)
No seu exercício, substituindo os valores a fórmula ficaria desta fórma:
4 / 8 = (16-h) / 16
Multiplicando cruzado:
64 = 128 - 8h
64 - 128 = -8h
-64 = -8h (x -1)
8h = 64
h = 64/8
h = 8
Sabendo a altura do cilindro, é só utilizara a fórmula para cálculo do volume:
V = ? . r² . h
V = 3,14 . 4 . 8
V = 68,48 m³
Espero que tenha te ajudado, qualquer coisa mande uma mensagem ou entre no meu perfil e solicite uma aula experimental.
Até a próxima!

Olá Vitória! Tudo bem? Vou tentar te ajudar, mas para isso, precisamos de mais um detalhe na redação da questão, que é a informação de que o cilíndro reto é ou não equilátero. Vamos assumir que o cilindro seja equilátero, neste caso há uma particularidade nesta figura, pois vale que h=2r. Como o raio do cilindro é a metade do raio da base do cone (que vale 8 cm), logo temos r=4cm. Por último, para calcularmos o volume do cilindro, usamos a relação: , (lembre que aqui h = 2r), daí chegamos substituindo chegamos à relação final:
. Substituindo r = 4 cm, encontramos
.
