Campo gravitacional no interior da Terra

Se você fizer um túnel retilíneo na Terra, ligando o Brasil ao Japão, como a gravidade irá variar conforme adentra este túnel?

Júlio Verne, que escreveu o livro "Viajem ao Centro da Terra", descreveu a gravidade aumentando conforme de descia para o centro e ao chegar o centro ela subtamente desaparecia. Esta é uma visão equivocada e o que faremos aqui, embora aproximado, será mais próximo da realidade do que a descrição de Júlio Verne.

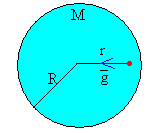
Primeiro, seja R o raio da Terra e r a distância do ponto de estudo neste túnel até o centro da Terra.

Sabe-se que o campo gravitacional no ponto de interesse depende apenas na massa interna à esfera de raio r.

Se assumirmos que a Terra possui uma densidade $\rho$ contante, massa M, a constante gravitacional for G, podemos calcular o campo gravitacional em função da posição r: $$g_{int}=\frac{G \cdot M_{int}}{r^2}=\frac{G}{r^2} \cdot \rho \cdot V_{int}=\frac{G \cdot \rho}{d^2} \frac{4}{3} \pi d^3 \Rightarrow$$ $$g_{int}=\frac{4G \pi r}{3} \cdot \rho =\frac{4G \pi r}{3} \cdot \frac{M}{\frac{4}{3} \cdot \pi R^3} \Rightarrow$$ $$\boxed{g_{int}=\frac{GM}{R^3}\cdot r}$$

Ou seja, o campo gravitacional diminui conforme aproximamos do centro da Terra.

Agora, imagine que resolvemos usar esse túnel para irmos do Brasil ao Japão. Se fosse possível eliminar completamente o atrito com o ar e com as superfícies, qual seria o tempo $\Delta t$ de ida do Brasil ao Japão? Repare que não haveria nenhum custo energético.

Para responder esta pergunta devemos comparar a equação da força elástica com a da força gravitacional. Repare que a força elástica é $$F_{el}=k\cdot x$$ enquanto que a força gravitacional será: $$F_{grav}=mg=\frac{GMm}{R^3}\cdot r$$ Em ambas as equações temos uma conatante multiplicando uma variável espacial, então podemos supor que a velocidade angular de ambos os casos obedecem à mesma equação: $$\omega = \sqrt{\frac{k}{m}}$$ Se compararmos as duas equações da força (elástica com gravitacional) encontramos que matematicamente $k=\frac{GMm}{R^3}$, assim para o corpo caindo no túnel: $$\omega = \sqrt{\frac{GM}{R^3}}=\frac{2\pi}{T}=\frac{2\pi}{2 cdot \Delta t }$$ Potanto: $$ \boxed { \Delta t = \pi \sqrt{ \frac{R^3}{GM} } }$$

Substituindo $ R = 6.400 \rm{km} $, $G = 6,67 \cdot 10^{-11} \frac{\rm{N}\cdot\rm{m}^2}{\rm{kg}^2} $, $\pi=3,14$ e $M=6,0\cdot10^{24}\rm{kg}$, temos: $$\boxed{\Delta t = 42 \rm{min}22\rm{s}}$$

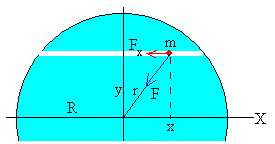
Poderíamos continuar com esta discussão e mnos questionar se o tempo de viagem seria menor se fizessemos um outro túnel paralelo ao primeiro mas que agora não passe pelo centro da terra conforme o esquema abaixo:

Surpreendentemente o período será o mesmo!

Seja $\theta$ o ângulo entre o vetor posição $r$ e o eixo y, então a abscissa $x$ será $r sin\theta$ e a força ao longo do eixo $x$ será $F_{grav} sin\theta$. Substituindo isso na equação da força gravitacional: $$F_x=F_{grav} sin\theta=\frac{GMm}{R^3}\cdot r sin\theta = \frac{GMm}{R^3}\cdot x$$ ou seja $$k=\frac{GMm}{R^3}$$ portanto o período será igual: $$\boxed{T=2\pi \sqrt{\frac{R^3}{GM}}}$$

$\boxed{}$

Artigo original em http://estudeadistancia.professordanilo.com/?p=335