![Equação de 2º Grau [1]](https://cdn.profes.com.br/images/categories/matematica.webp)
INTRODUÇÃO
Equação de Segundo grau, contrário ao que alguns pensam, é muito utilizada em diversas funções, concursos públicos e vestibulares, por este motivo, tão cobrada no Ensino Médio e no 8º e 9º ano do Ensino Fundamental; neste período, alguns alunos apresentam um certo medo, pela sua complexividade, mas após o domínio, se torna algo tão simples e fácil.
Você sabia que a Equação de 2º Grau é utilizada na Bovespa para determinar os pontos de entrada, saída, ponto médio, gaps, pontos de Stops, Suporte e Resistência em uma operação de investimento? Em outro artigo irei falar sobre isso... Mas a Equação vai além disto, determina na física o lançamento vertical para cima, na matemática determina a Parábola e seus pontos, e vai muito além. Dá até para calcular se um chute de pênalti vai acertar no Gol ou fora. ;)
Mas afinal, o que é a Equação de Segundo Grau?
Simples, a Equação é determinada por esta fórmula ax²+bx+c (é determinada segundo grau, só por causa daquele "2" em cima do "X" #ficaadica se ver o quadrado é segundo grau), onde "a", "b" e "c" são números e "X" são as raízes da equação
Você sabia que isto foi uma pergunta da EEAR de 2006? (A prova da Escola de Especialista da Aeronáutica perguntava qual determinava a equação de segundo grau).
Certo, e da onde vem essa fórmula da equação de segundo grau?
Geralmente você pode em algum momento da sua vida de estudos ter pego ou ainda irá pegar algo parecido com isso: (2+X).(4+X) [neste caso eu coloquei números aleatórios, só para você entender que vai ser dois parênteses com X multiplicando entre eles]
Para resolver devemos aplicar uma distributiva em que o (2) multiplica o (4 e o X), e o (+X) multiplica o (4 e o X), ficando (2.4)+(2.X)+(X.4)+(X.X) -> 8+6X+X² em que A=1 (não tem nada do lado do X², então é 1 imaginário) B=6 e C=8 FIQUE ATENTO, AQUI ESTÁ INVERTIDA, MAS DÁ NO MESMO. ;)
Então você está vendo os exercícios que precisam ser feitos e se depara com a seguinte pergunta: Determine mediante ao gráfico da parábola numa função quadrangular as raízes que determinam a seguinte equação X² - 7X - 8
Dica: Toda vez que você ouvir ou ver ou ler "raízes" numa equação, nada mais é do que o X, ou seja, determine o X; mas atenção, como é uma equação quadrática, quadrangular, quadrada, enfim... É uma equação de segundo grau, e neste caso, as raízes possuem 2 resultados. No próximo artigo desta série entrarei em detalhes, pois existem questões de concursos públicos que fazem questão de mencionar que você deve considerar apenas números N, ou apenas Z, ou apenas positivos, e assim vai...
Resolvendo isso, decore para sua vida 
(chamamos esse triângulo de delta) = b²-4.a.c então vamos lá B é (-7) [da equação ali em cima; ah e atenção com o sinal, pelo amor, esse sinal muda tudo] A é 1 e C é -8 então vamos lá, na fórmula de Delta (-7)²-4.1.(-8) -> 49-(-32) [7 ao quadrado é 49; atenção com os sinais, cuidado que pega muitos jovens de surpresa na hora de responder rápido a questão do concurso] DELTA = 81
Agora que temos Delta, vamos para Bháskara (Bháskara foi um grande matemático, estudioso antigo, que criou esta fórmula)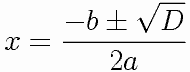 
percebe que tem dois sinais ali do lado da raíz de DELTA? um (+) e um (-)? então...
Como são duas raízes, começamos com X1= [- (-7) + V81]/2.1
Raíz² de 81 é 9 + 7 [olha os sinais de novo] =16/2
X1=8
agora que usamos o (+), repetimos a fórmula usando o (-) então X2
X2= [-(-7) - V81]/2.1
Raíz já sabemos é 9, neste caso tem um sinal negativo na frente da raíz então vai ser (7-9)/2 = -1
X2=-1
Portanto: "Determine mediante ao gráfico da parábola numa função quadrangular as raízes que determinam a seguinte equação X² - 7X - 8"
As raízes que determinam a equação são 8 e -1 ou para ficar mais bonito S={X£Z/X1=8 e X2=-1} Em outro artigo entrarei em detalhe sobre essa forma de resposta (pois ela é usada em vestibulares federais e de grandes universidades como USP)
Prontinho já determinados a Equação de Segundo Grau, delta e bháskara e determinados suas raízes, no próximo artigo iremos aprofundar mais.
E que tal como teste para ver se compreendeu, determinar qual o conjunto das raízes daquela primeira equação lá em cima?
essa aqui -> 8+6X+X² fica o desafio ;)
Aulas particulares
Buscar
Atividades acadêmicas
Pedir
Tira-dúvidas com IA
Enviar dúvida
Ver WhatsApp
