Aulas particulares Tarefas Minerva IA Entrar Criar conta

EMPUXO DE TERRA PELA TEORIA DE RANKINE

Autor: Rafael D.

Engenharia

10/04/23

Profes / Blog / Engenharia

Geral

Resolução de Exercicio

Exemplo resolvido

Para a melhor fixação do conteúdo abordado no post, calcularemos a resultante do empuxo ativo para o exemplo abaixo.

Resolva exercícios e atividades acadêmicas

Envie atividades, projetos ou exercícios para um professor resolver no seu prazo.

1º Passo

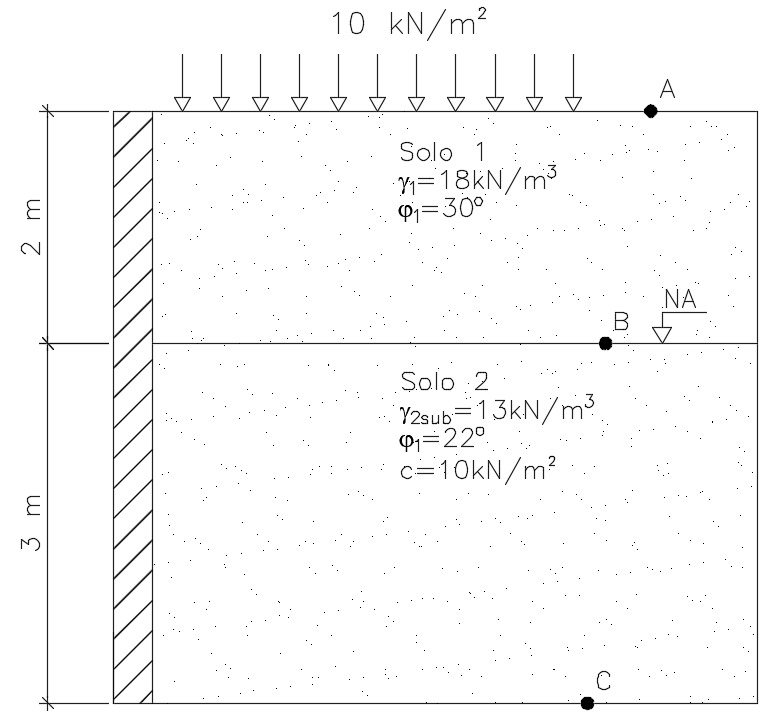
O primeiro passo para a resolução do problema é a determinação das tensões verticais efetivas nos pontos A, B e C, determinados na imagem da questão.

Então, temos que a tensão no ponto A será a da sobrecarga. No ponto B será a soma da sobrecarga com o peso próprio do solo até aquela profundidade e no ponto C será a tensão do no ponto B somada ao peso próprio do solo 2 submerso. Logo:

$σ_{v A} = 10 k N / m^{2}$

Encontre o professor particular perfeito

$σ_{v B} = 10 + 18 \cdot 2 = 46 k N / m^{2}$

$σ_{v C} = 46 + 13 \cdot 3 = 85 k N / m^{2}$

Agora que já sabemos às tensões nos pontos, devemos determinar o coeficiente de empuxo ativo para os solos 1 e 2. Teremos então, segundo a teoria de Rankine:

$k_{a 1} = tan^{2} (45 - 30 / 2) = 0, 33$

Tutoria com Inteligência Artificial

Tecnologia do ChatGPT. Use texto, áudio, fotos, imagens e arquivos.

$k_{a 2} = tan^{2} (45 - 22 / 2) = 0, 45$

2º Passo

De posse desses dados, já podemos calcular a tensão horizontal atuante nos pontos A, B e C. Lembrando que para o ponto B devemos determinar a tensão horizontal para o solo 1 e para o solo 2 e que no cálculo da tensão para o solo 2 devemos considerar a coesão do mesmo e o peso da água no trecho. Temos então:

$σ_{h A} = σ_{v A} \cdot k_{a 1} = 10 \cdot 0, 33 = 3, 3 k N / m^{2}$

$σ_{h B 1} = σ_{v B} \cdot k_{a 1} = 46 \cdot 0, 33 = 15, 2 k N / m^{2}$

$σ_{h B 2} = σ_{v B} \cdot k_{a 2} - 2 \cdot c k^{a 2}$

$σ_{h B 2} = 46 \cdot 0, 45 - 2 \cdot 10 0, 45 = 7, 3 k N / m^{2}$

$σ_{h C} = σ_{v C} \cdot k_{a 2} - 2 \cdot c k^{a 2} + γ_{a ˊ g u a} \cdot 3$

$σ_{h C} = 85 \cdot 0, 45 - 2 \cdot 10 0, 45 + 30 = 54, 8 k N / m^{2}$

Pronto! Agora nós já podemos montar o diagrama de tensões horizontais atuantes na contenção. Temos então o seguinte gráfico:

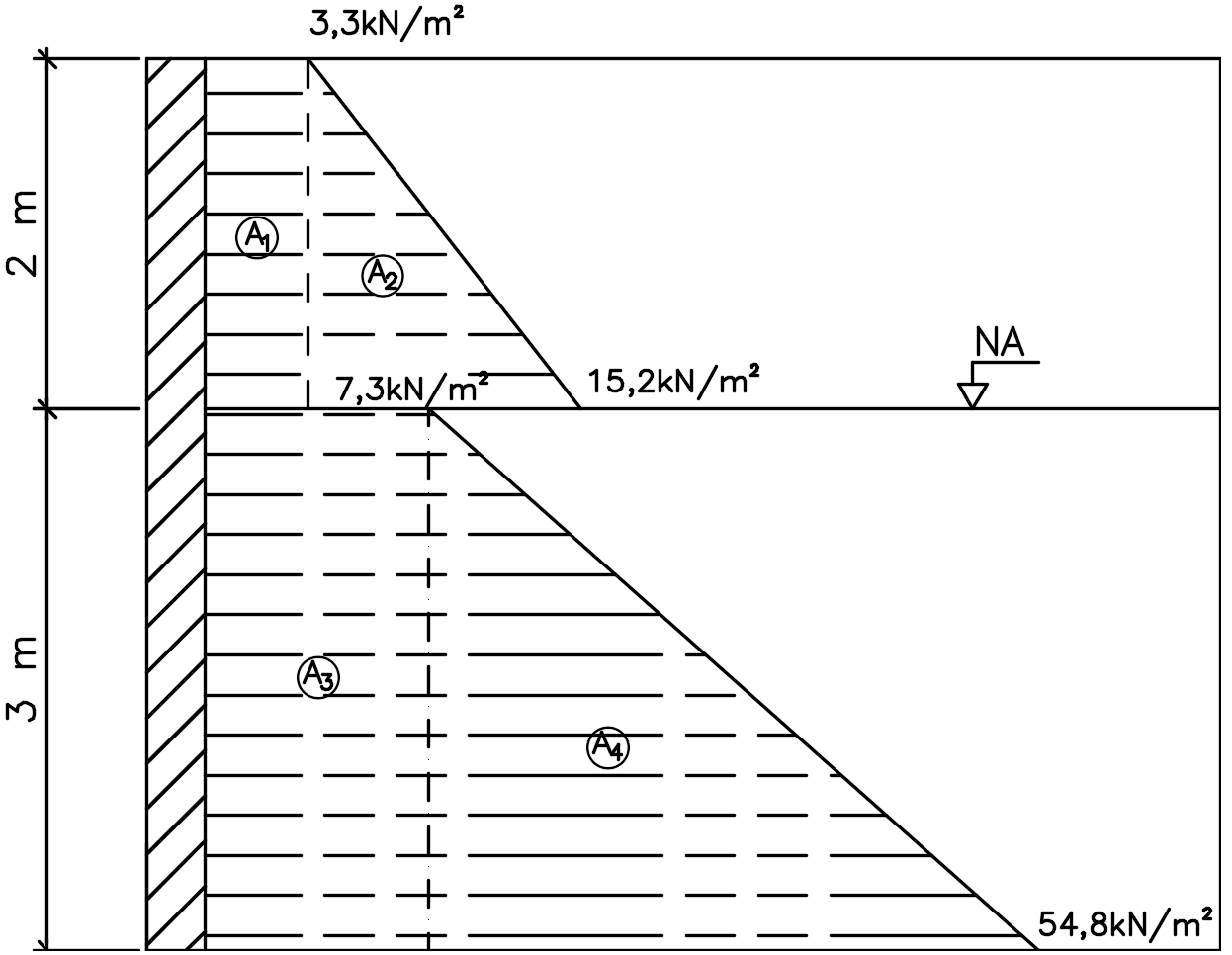
Para realizarmos o cálculo do empuxo resultante, devemos apenas calcular o volume desse prisma de tensões. Considerando a largura do prisma como sendo 1,0 metro, consideração bastante usual no cálculo de contenções, basta calcular a área do gráfico apresentado acima que teremos o empuxo para 1,0 metro de contenção.

3º Passo

Como você já percebeu, eu as áreas foram subdivididas em quatro áreas menores para facilitar tanto o cálculo do empuxo quanto a posição dessa força resultante. Vamos então calcular o empuxo para cada área já demarcada acima.

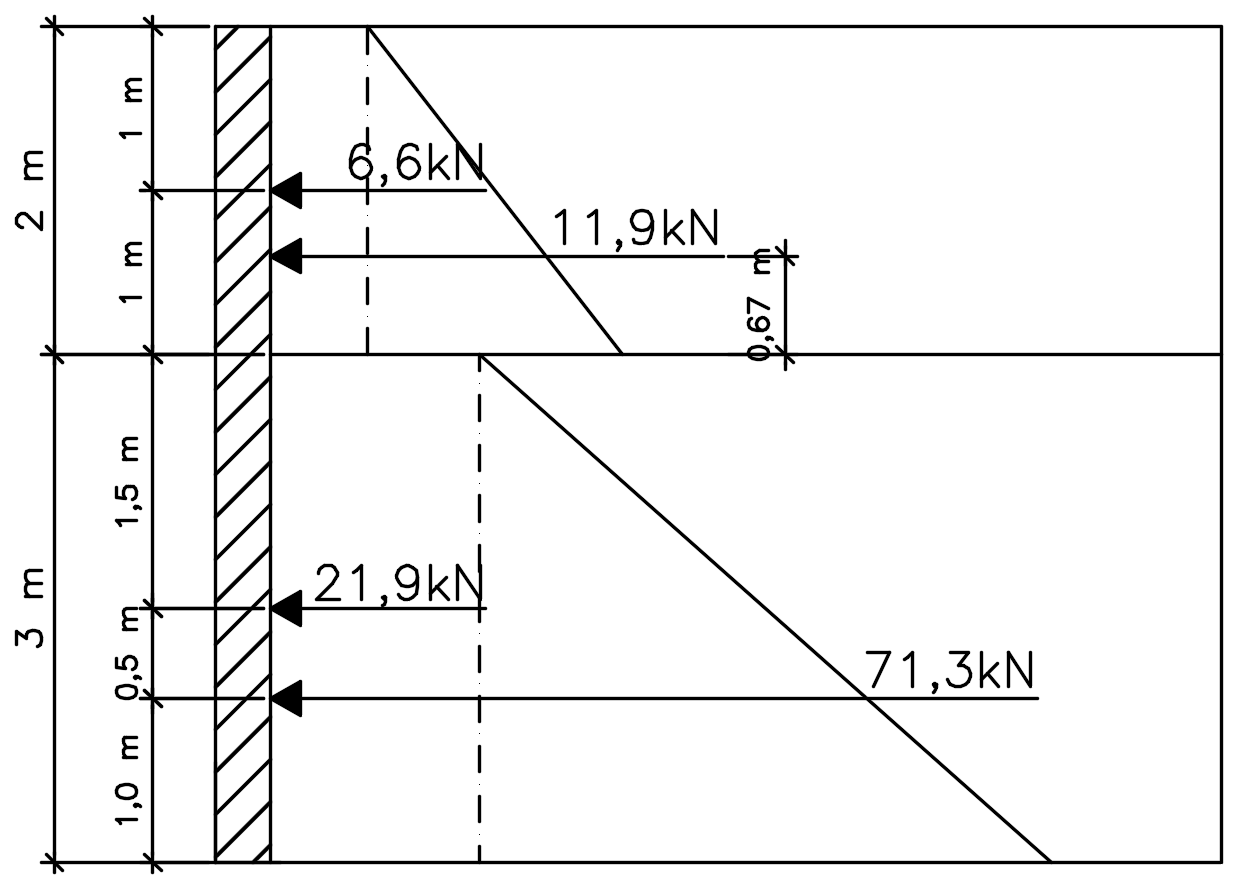
$E_{A 1} = 3, 3 \cdot 2, 0 = 6, 6 k N$

$E_{A 2} = 2 ( 1 5 , 2 - 3 , 3 ) \cdot 2 , 0 = 11, 9 k N$

$E_{A 3} = 7, 3 \cdot 3, 0 = 21, 9 k N$

$E_{A 4} = 2 ( 5 4 , 8 - 7 , 3 ) \cdot 3 , 0 = 71, 3 k N$

Pronto, já calculamos o empuxo ativo total atuante na contenção, agora para finalizar, vamos apenas determinar o ponto de aplicação desses empuxos de terra, que será o centroide de cada prisma de tensões. Teremos então o seguinte esquema: