Efeito fotoelétrico (Química e Física)

EFEITO FOTOELÉTRICO

Olá! Vou disponibilizar um assunto que já foi questão do vestibular do ITA, e é muito visto em curso especiais devido a sua importância: o Efeito Fotoelétrico.

A constante h, hoje conhecida como constante de Planck, é igual a 6,626x10^34 J·s. Se os átomos, ao oscilar, transferem a energia E para a vizinhança, detecta-se radiação de frequência V= E/h.
A hipótese de Planck sugere que radiação de frequência V só pode ser gerada se um oscilador com essa frequência tiver a energia mínima suficiente para começar a oscilar. Em temperaturas baixas, não existe energia suficiente para estimular a oscilação em frequências muito altas, e o objeto não pode gerar radiação ultravioleta, de alta frequência. Na física clássica, ao contrário, considerava-se que um objeto poderia oscilar com qualquer energia e, portanto, mesmo em temperaturas baixas, os osciladores de alta frequência poderiam contribuir para a radiação emitida. 

Para desenvolver essa teoria de sucesso, Planck teve de descartar a física clássica, que não restringe a quantidade de energia que pode ser transferida de um objeto para outro. Ele propôs descrever a transferência de energia em termos de pacotes discretos. Para justificar uma revolução tão drástica, no entanto, outras evidências eram necessárias. Uma delas vem do efeito fotoelétrico, a ejeção de elétrons de um metal quando sua superfície é exposta à radiação ultravioleta. As observações experimentais são:

1 Nenhum elétron é ejetado até que a radiação tenha frequência acima de um determinado valor, característico do metal.

2 Os elétrons são ejetados imediatamente, por menor que seja a intensidade da radiação.

3 A energia cinética dos elétrons ejetados aumenta linearmente com a frequência da radiação incidente.

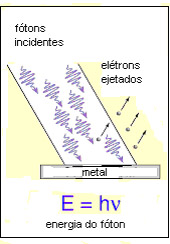
Figura 1.1: radiação incidente no metal acima de determinada frequência provoca ejeção de elétrons.

Albert Einstein encontrou uma explicação para essas observações e, no processo, modificou profundamente nossa concepção do campo eletromagnético. Ele propôs que a radiação eletromagnética é feita de partículas, que mais tarde foram chamadas de fótons. Cada fóton pode ser entendido como um pacote de energia, e a energia do fóton relaciona-se com a frequência da radiação pela Eq. (E = hV). Assim, por exemplo, os fótons da luz ultravioleta têm mais energia do que os fótons da luz visível, que têm frequências menores. De acordo com esse modelo de fótons para a radiação eletromagnética, pode-se visualizar um feixe de luz vermelha como um feixe de fótons com uma dada energia, a luz amarela como um feixe de fótons de energia maior e a luz verde como um feixe de fótons de energia mais alta ainda. É importante notar que a intensidade da radiação é uma indicação do número dos fótons presentes e que E =hV é uma medida da energia de cada fóton, tomado individualmente.

As características do efeito fotoelétrico são facilmente explicadas se considerarmos a radiação eletromagnética em termos de fótons. Se a radiação incidente tem frequência V, ela é formada por um feixe de fótons de energia hV. Essas partículas colidem com os elétrons do metal. A energia necessária para remover um elétron da superfície de um metal é chamada de função de trabalho do metal e representada pela letra grega fi maiúsculo. Se a energia do fóton é inferior à energia necessária para remover um elétron do metal, não ocorrerá a ejeção do elétron, independentemente da intensidade da radiação. Se a energia do fóton, hV, é maior do que fi maiúsculo, então um elétron com energia cinética Ec = mev²/2, igual à diferença de energia do fóton e a função de trabalho, Ec = hV - fi maiúsculo, é emitido. Segue-se que

Equação 1.1: equação característica do efeito fotoelétrico

Como a energia cinética dos elétrons ejetados varia linearmente com a frequência, um gráfico da energia cinética contra a frequência da radiação deveria se parecer com o gráfico da Fig. 1.2, uma linha reta de inclinação igual a h, que é a mesma para todos os metais e com interseção com o eixo vertical em -fi maiúsculo, característica do metal. A interseção com o eixo horizontal (que corresponde a um elétron ejetado com energia cinética igual a zero) é sempre igual a fi maiúsculo/h.

Agora, podemos interpretar os resultados experimentais do efeito fotoelétrico à luz da teoria de Einstein:

1 Um elétron só pode ser expelido do metal se receber do fóton, durante a colisão, uma quantidade mínima de energia igual à função de trabalho, fi maiúsculo. Assim, a frequência da radiação deve ter um valor mínimo para que elétrons sejam ejetados. Essa frequência mínima depende da função de trabalho – logo, da natureza do metal (Fig. 1.2).

2 Se o fóton tem energia suficiente, a cada colisão observa-se a ejeção imediata de um elétron.

3 A energia cinética do elétron ejetado do metal aumenta linearmente com a frequência da radiação incidente, de acordo com a 1.1.

Figura 1.2: energia em função da frequência no efeito fotoelétrico.

REFERÊNCIAS

W., ATKINS, Peter, and JONES, Loretta. Principios de Química - Questionando a vida moderna e o meio, 5ª edição. Bookman, 2012. VitalBook file.