Por: Prof R. 02 de Agosto de 2018
O que é a mediana?
Estatística Ensino Fundamental Profissional Faculdade Aulas De Reforço Ensino superior Probabilidade Avançado Básico ENEM Ensino Médio Curso superior Concurso Vestibular Estatística Básica
Encontre um professor e combine aulas particulares Presenciais ou Online
A mediana indica o valor que está exatamente no meio de um conjunto de dados, quando eles estão ordenados do menor valor para o maior. A Mediana nos diz que metade (50%) dos valores do conjunto de dados está abaixo dela e a outra metade está acima dela. No geral, o termo mediana se refere ao que está entre dois pontos, dois extremos.
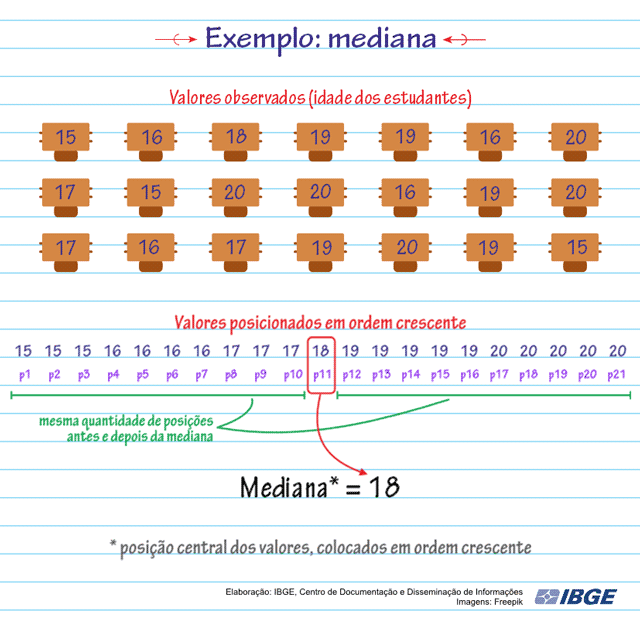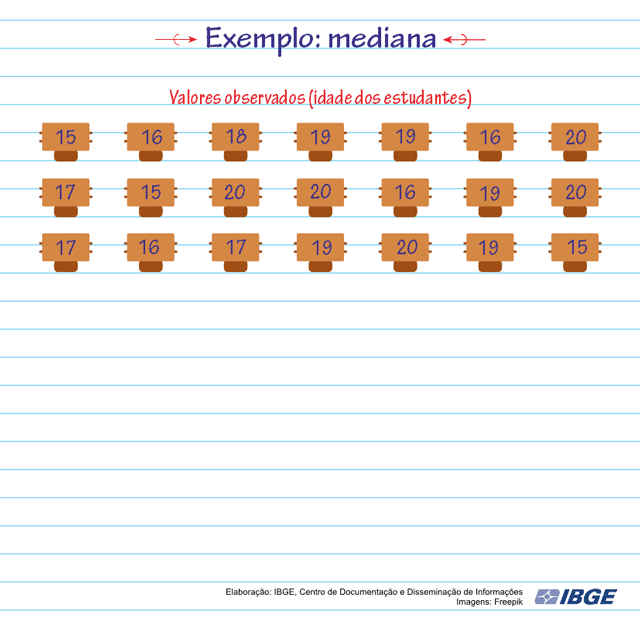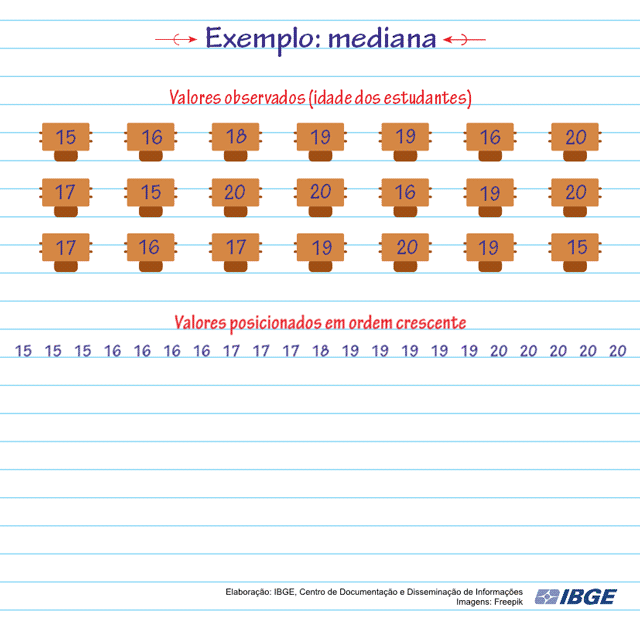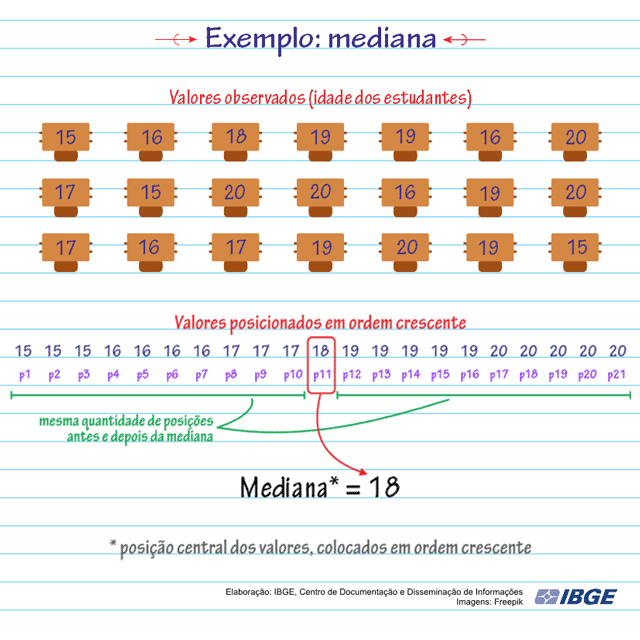
Em uma sala de aula foi realizada uma pesquisa onde uma das perguntas era a idade dos alunos. Confira na animação o cálculo da mediana das idades dos alunos:
Observe que: i) cada idade ocupa uma posição (de p1 até p21), no conjunto de dados; ii) as idades estão ordenadas do menor valor para o maior; iii) a mediana será a idade 18 anos, porque ela se encontra exatamente na 11ª posição (p11), o meio do conjunto de dados. Podemos observar que metade das idades é menor que 18 e a outra metade das idades é maior que 18.
- Se você tem um conjunto de informações, então a Mediana, que é uma medida de tendência central, indicará exatamente a posição onde será encontrado o valor da amostra que está eqüidistante aos extremos;
- A Mediana nos diz que a quantidade de valores é a mesma tanto antes quanto depois de sua posição;
- A vantagem da Mediana sobre a Média é que a Mediana pode nos fornecer um valor típico do conjunto de dados porque ela não é afetada por valores extremos;
- Podemos considerar a Mediana como uma Média quando o conjunto de dados não é influenciado por valores extremos ou quando há poucos valores extremos, tanto altos quanto baixos.
- Se a quantidade de elementos da amostra (conjunto de dados) for uma quantidade ímpar, então a amostra terá um elemento central e a Mediana será o elemento que se encontra na posição: (Número de elementos da amostra + 1) / 2;
- Se a quantidade de elementos da amostra for uma quantidade par, então a amostra terá dois elementos centrais e a Mediana será a média aritmética entre eles. Então, como encontrar a posição dos elementos da amostra para calcular a média entre eles? Primeiro elemento: (Número de elementos da amostra) / 2; e segundo elemento: o resultado do primeiro elemento + 1.
Exemplo de cálculo da mediana com número ímpar de elementos na amostra
Vamos encontrar a Mediana da população rural do Brasil no Censo de 2010:
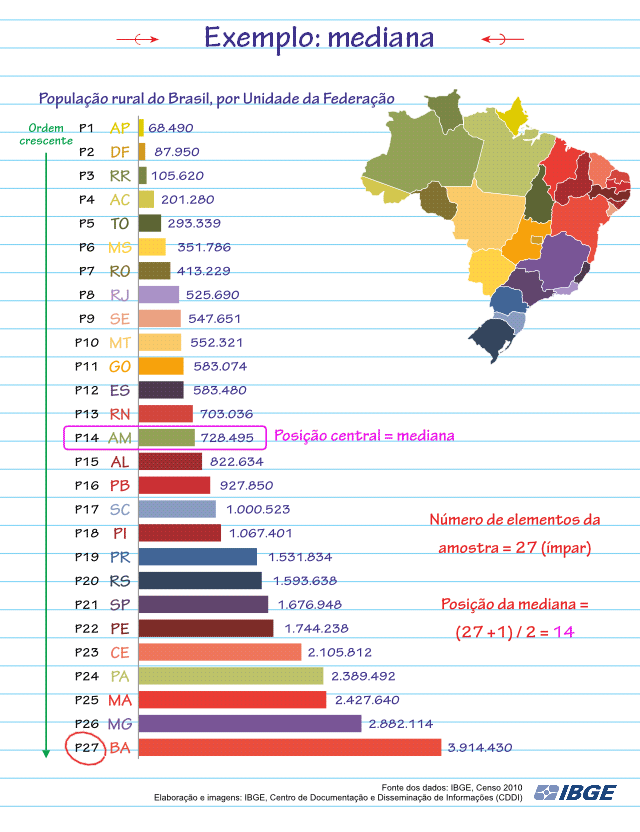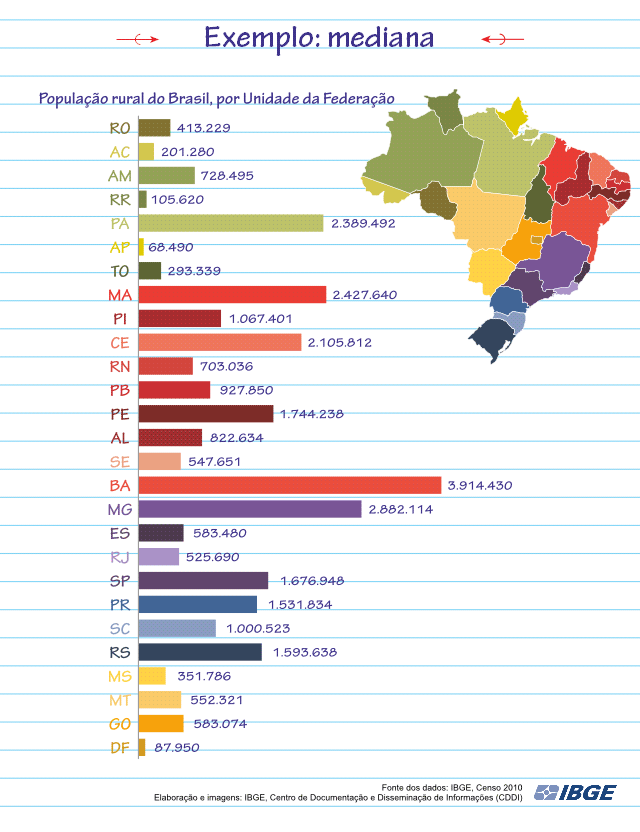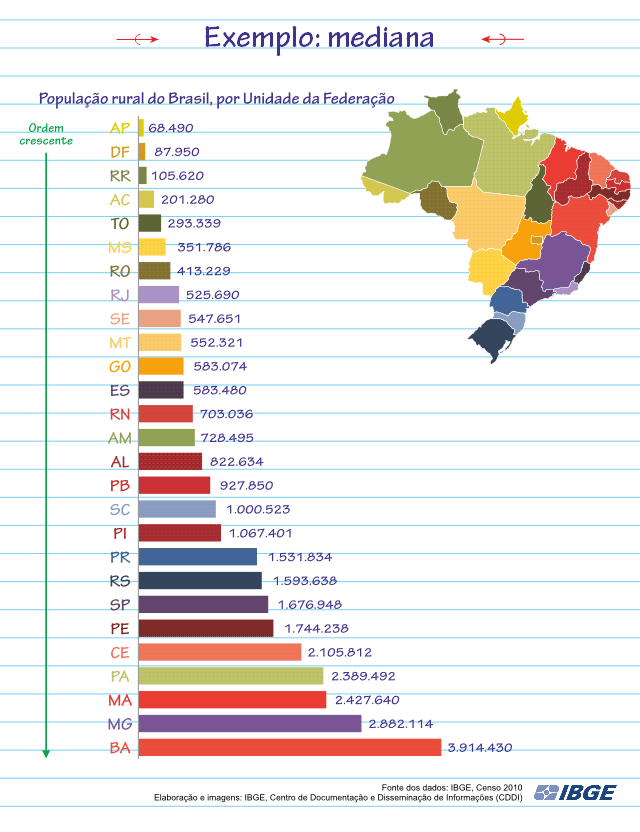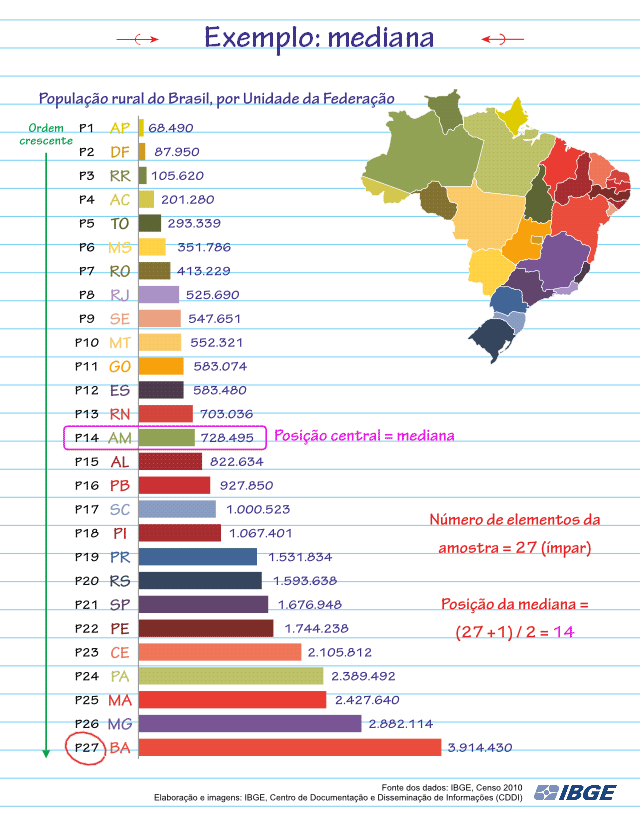
Como pode ser visto na animação, o valor da Mediana será 728.495. Que informação nos fornece esta Mediana? Ela nos diz que metade dos Estados do Brasil possui população rural menor ou igual a 728.495 e a outra metade possui população rural maior ou igual a 728.495.
Colocar o conjunto de dados (a nossa amostra) em uma ordem crescente para poder encontrar a Mediana nos revela outras duas informações também importantes: o Valor Mínimo e o Valor Máximo da amostra. A Mediana se encontra exatamente entre o Valor Máximo − que é o último da amostra em ordem crescente − e o Valor Mínimo da amostra, que é o primeiro da amostra em ordem crescente.
No exemplo dos Estados da Federação, o Estado que possui a menor população rural (Valor Mínimo da amostra) é o Amapá, com 68.490 habitantes, e o Estado que possui a maior população rural (Valor Máximo da amostra) é a Bahia, com 3.914.430 habitantes.
Vamos, agora, utilizar um exemplo onde o número de elementos do conjunto de dados seja par. Utilizemos o conjunto de dados formado pelo número de habitantes existentes nos municípios do Estado do Rio de Janeiro, conforme o Censo de 2010. A quantidade de municípios é de 92. A tabela com os dados dos municípios está disponível neste link.
Lembre-se que: se a quantidade de elementos da amostra for uma quantidade par, então a amostra terá dois elementos centrais e a Mediana será a Média Aritmética entre eles. Devemos, então:
- Colocar os dados em ordem crescente;
- Encontrar o primeiro elemento da amostra para o cálculo da Mediana: elemento da amostra que se encontra na posição 46: 34.410 (quantidade de residentes do município de Vassouras);
- Encontrar o segundo elemento da amostra para o cálculo da Mediana: informação da amostra que se encontra na posição 47: 35.347 (quantidade de residentes do município de Casimiro de Abreu);
- A Mediana será a média aritmética entre esses dois valores: (34.410 + 35.347) / 2 = 34.878,5
Passamos a saber que:
- Valor Mínimo: 5.269 − O município de Macuco possui a menor quantidade de habitantes do Estado do Rio de Janeiro; Valor Máximo: 6.320.446 − O município do Rio de Janeiro possui a maior quantidade de habitantes do Estado do Rio de Janeiro;
- Como a Mediana é 34.878,5, então:
- Metade (50%) dos municípios do RJ possui quantidade de habitantes menor que 34.878,5, e;
- A outra metade (50%) possui a quantidade de habitantes maior que 34.878,5;
- O valor 34.878,5 não faz parte do conjunto de dados (amostra).
