O primeiro conjunto a surgir naturalmente no decorrer da historia da humanidade foi o conjunto dos números naturais representados por  .Esse conjunto está associado a ideia natural de contar os objetos.
.Esse conjunto está associado a ideia natural de contar os objetos. ={ 0; 1 ;2;3;....}
={ 0; 1 ;2;3;....}
* ={ 1 ;2;3;....}
={ 1 ;2;3;....}
O * em cima do N significa não nulo ou seja sem contar o numero zero.
O ... representa que esse conjunto continua infinitamente.
O segundo conjunto a surgir foi o conjunto dos números inteiros representados por  .Neste conjunto está presente somente números inteiros.A novidade desse conjunto é a presença de números negativos e regras de sinas para soma e multiplicação.
.Neste conjunto está presente somente números inteiros.A novidade desse conjunto é a presença de números negativos e regras de sinas para soma e multiplicação. ={ ...;-3 ; -2 ; -1; 0; 1 ;2;3;....}
={ ...;-3 ; -2 ; -1; 0; 1 ;2;3;....} C
C 
Logo todo numero natural também é um numero inteiro porém nem todo inteiro é natural.
O terceiro conjunto a surgir foi o conjunto dos números racionais representados por  .Os números racionais são os números que podem ser escritos na forma de a/b .A novidade desse conjunto é a presença de algumas frações e o surgimento de números decimais.
.Os números racionais são os números que podem ser escritos na forma de a/b .A novidade desse conjunto é a presença de algumas frações e o surgimento de números decimais.
Exemplos de números racinais são 1/2, 0,15 ... Um exemplo de representação de um conjunto de racionais seria: ={ -3;-2,5 ; -2 ; -1; 0; 1/2; 1 ;2;3;....}
={ -3;-2,5 ; -2 ; -1; 0; 1/2; 1 ;2;3;....}
O quarto conjunto a surgir foi o conjunto dos números irracionais representados por  Os números irracionais são números que não podem ser escritos como a/b.Exemplos de números irracionais são
Os números irracionais são números que não podem ser escritos como a/b.Exemplos de números irracionais são  ,o numero PI ,o numero aureo que aparece na proporção do corpo humano e diversos lugares na natureza. Se numero tem decimais diferentes e uma soma infinita divergente então é irracional pois não pode ser representado por a/b onde a e b são inteiros.Existem numero que possuem uma soma infinita de termos e podem ser representados como a/b um exemplo disso é a soma dos termos infinitos de uma P.G.Outros exemplos são as funções tradicionais escritas em expansões de series de Taylor...e voltando ao tema central..
,o numero PI ,o numero aureo que aparece na proporção do corpo humano e diversos lugares na natureza. Se numero tem decimais diferentes e uma soma infinita divergente então é irracional pois não pode ser representado por a/b onde a e b são inteiros.Existem numero que possuem uma soma infinita de termos e podem ser representados como a/b um exemplo disso é a soma dos termos infinitos de uma P.G.Outros exemplos são as funções tradicionais escritas em expansões de series de Taylor...e voltando ao tema central..
Por exemplo
√2 = 1,4142135 ... irracional
√3 = 1,7320508 ... irracional
Porém esses exemplos:
0,333333333333333333 é racional pois pode ser escrito como 1/3
0,1111111111111111111111110000000000 é racional pois pode ser escrito como 111111111111111111111111/100000000000000000000000
Até agora temos que  C
C  C
C  porém o
porém o  não faz parte dos conjuntos anteriores.A soma de todos os conjuntos
não faz parte dos conjuntos anteriores.A soma de todos os conjuntos  ,
,  ,
,  e
e  forma o conjunto
forma o conjunto
dos números reais ou  .Os números reais podem ser representados por uma reta e por isso o
.Os números reais podem ser representados por uma reta e por isso o  tem dimensão 1.
tem dimensão 1.
Porém os primeiros a darem soluções para as equações cubicas(ax³+bx²+cx+d) são foram Scipione del Ferro e Tartaglia e com isso aparece os números complexos porém Descartes, no século XVII, os chamou de números imaginários pois estes não tinha grande importância para época.Atualmente os numeros imaginários tem varias aplicações praticas em fenômenos como eletricidade por exemplo.Existe uma versão estendida da lei de ohm u=r*i utilizando números complexos.
Os números complexos são representados por  . UM numero é complexo se z=a+bi onde a e b pertencente aos reais e i é uma unidade imaginaria tal que i²=-1. Quando se passa dos números reais para os complexos é perdida a propriedade da ordem justamente porque os
. UM numero é complexo se z=a+bi onde a e b pertencente aos reais e i é uma unidade imaginaria tal que i²=-1. Quando se passa dos números reais para os complexos é perdida a propriedade da ordem justamente porque os  podem ser representados por um plano e como o plano tem 2 dimensões então
podem ser representados por um plano e como o plano tem 2 dimensões então  tem dimensão 2.As dimensões que conhecemos usuais são comprimento,altura e largura ou 3D(dimensões).Por essa razão era provável que o próximo conjunto de numero
tem dimensão 2.As dimensões que conhecemos usuais são comprimento,altura e largura ou 3D(dimensões).Por essa razão era provável que o próximo conjunto de numero  tivesse dimensão 3.
tivesse dimensão 3.
Um irlandês chamado willian Rowan Hamiton nascido em 1805 em dublin passou vários anos de sua vida tentando descobrir o conjunto  com dimensão 3 porém sem sucesso.Após 10 anos tentou o mesmo problemas com 4 dimensões e para sua surpresa ele conseguiu uma resposta.Então ele pegou seu canivete e com ele gravou sua teoria fundamental da tábua de multiplicação dos quatérnios numa das pedras da Ponte Brougham na Irlanda.Atualmente existe uma placa que tem o registro dessa historia nessa cidade .Atualmente muitas pessoas usam esse tipo de numero sem saber que usa quando faz conta com VETORES pois os vetores tem propriedades semelhantes ao
com dimensão 3 porém sem sucesso.Após 10 anos tentou o mesmo problemas com 4 dimensões e para sua surpresa ele conseguiu uma resposta.Então ele pegou seu canivete e com ele gravou sua teoria fundamental da tábua de multiplicação dos quatérnios numa das pedras da Ponte Brougham na Irlanda.Atualmente existe uma placa que tem o registro dessa historia nessa cidade .Atualmente muitas pessoas usam esse tipo de numero sem saber que usa quando faz conta com VETORES pois os vetores tem propriedades semelhantes ao 
O simbolo  representa o numero dos quaternários.Este conjunto é definido como:
representa o numero dos quaternários.Este conjunto é definido como:
Resolva exercícios e atividades acadêmicas
Onde a,b,c,e são números reais 
e i,j,k obedecem as seguintes regras.
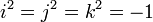
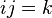 |
 |
 |
 |
 |
 |
Portando o  tem dimensão 4.Um fato curioso de
tem dimensão 4.Um fato curioso de  é que não existe mais comutatividade no produto pois
é que não existe mais comutatividade no produto pois
i x j= k e j x i= -k .Assim isso é um indicio de que quando você dobra a dimensão você perde uma propriedade matemática.Por exemplos de  para
para  a dimensão dobrou de 1 para 2 então perdeu-se a propriedade da ordem.Por exemplo em
a dimensão dobrou de 1 para 2 então perdeu-se a propriedade da ordem.Por exemplo em  você pode falar que um numero é maior ou menor que outro porém em
você pode falar que um numero é maior ou menor que outro porém em  não existe um numero complexo maior que outro pois a propriedade de ordem foi perdida pois não faz sentido falar que um vetor é maior que outro pois para caracterizar um vetor é preciso modulo,direção e sentido.
não existe um numero complexo maior que outro pois a propriedade de ordem foi perdida pois não faz sentido falar que um vetor é maior que outro pois para caracterizar um vetor é preciso modulo,direção e sentido.
De  para
para  a dimensão dobrou de 2 para 4 então foi perdida a propriedade da comutatividade da multiplicação.
a dimensão dobrou de 2 para 4 então foi perdida a propriedade da comutatividade da multiplicação.
Encontre o professor particular perfeito
Esse conjunto  se a=0, assume a forma Q=bi+cj+ek que representa um vetor em 3 dimensões e tem propriedades bastante semelhantes ao produto vetorial e álgebra de vetores.
se a=0, assume a forma Q=bi+cj+ek que representa um vetor em 3 dimensões e tem propriedades bastante semelhantes ao produto vetorial e álgebra de vetores.
Mais tarde surgiu o conjunto 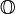 .Este conjunto representa os números octernarios ou octeniões.Estes teriam a dimensão 8 e teriam um construção semelhante aos
.Este conjunto representa os números octernarios ou octeniões.Estes teriam a dimensão 8 e teriam um construção semelhante aos  .Basta imaginar um numero
.Basta imaginar um numero
Q=a+bi+cj+dk+el+fm+gn+hp
em que a,b,c,d,e,f , g e h são reais e i,j,k,l,m,n e p são numeros tal que i²=j²=k²=l²=m²=n²= p²=-1
Porém neste conjunto 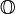 se perderia a propriedade da associatividade.Perder a associatividade significa que (2 x 3) x 4 seria diferente de 2 x( 3 x 4) pois não existe mais associatividade.
se perderia a propriedade da associatividade.Perder a associatividade significa que (2 x 3) x 4 seria diferente de 2 x( 3 x 4) pois não existe mais associatividade.
O próximo conjunto teria dimensão 16 e seria representado por 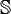 .Porém neste conjunto não é valida a divisão entre números.Então quando dobra a dimensão de 8 para 16 se perde a capacidade de fazer divisão.Muita calma já estamos muito além dos complexos e será que esses conjuntos tem realmente alguma utilidade.O
.Porém neste conjunto não é valida a divisão entre números.Então quando dobra a dimensão de 8 para 16 se perde a capacidade de fazer divisão.Muita calma já estamos muito além dos complexos e será que esses conjuntos tem realmente alguma utilidade.O 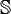 conjunto tem propriedade semelhantes a álgebra matricial pois ao trabalhar com matrizes não é permitido divisão entre matrizes.Então será que quando nós fazemos multiplicação de matrizes e aqueles contas malucas com determinantes já estaríamos usando esses conjuntos além dos números complexos como o
conjunto tem propriedade semelhantes a álgebra matricial pois ao trabalhar com matrizes não é permitido divisão entre matrizes.Então será que quando nós fazemos multiplicação de matrizes e aqueles contas malucas com determinantes já estaríamos usando esses conjuntos além dos números complexos como o 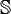 ?
?



