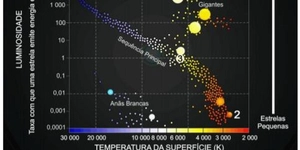
Lei da Gravitação de Newton

Lei da Gravitação de Newton

Newton foi o primeiro a formular uma teoria matemática da Gravidade. Essa teoria partiu da hipótese  de que se a 
Terra exerce uma força de atração sobre os objetos na Terra, então  essa força atrativa poderia se estender à Lua. 
Portanto a Terra exerceria uma força de atração sobre a  Lua produzindo uma aceleração centrípeto que manteria  a Lua em órbita. 
Logo, essa ideia poderia ser aplicada para os outros astros. Essa força de atração é proporcional a suas massas e inversamente 
proporcional ao quadrado da distância entre eles, 

Quanto maior as massas dos corpos e menor a distância entre eles, maior será a força gravitacional. Portanto, a lei gravitacional de Newton é 
descrita matematicamente por:

, é a constante gravitacional . A força gravitacional é uma força radial, podendo ser descrita por:

Essa é a equação que descreve a atração que os corpos exercem sobre o outro. Como a força gravitacional é uma força radial, 
ou seja uma força voltada para o centro, podemos determinar uma equação de movimento relativo de dois corpos. 
Partindo da equação  podemos descrever a força em : 

Pela terceira lei de Newton, temos que a força em :

Derivando a eq. abaixo em relação ao tempo duas vezes teremos a aceleração relativa do dois corpos,

Agora podemos substituir  e  em , para obter uma equação de movimento:

Chegamos na equação diferencial vetorial do movimento relativo de dois corpos. A solução descreve como o raio vetor  varia com o tempo. 
Sua solução não é simples, pois seria necessário seis constantes para obter a solução, caso tivéssemos a posição tridimensional e a velocidade 
de um planeta em um certo tempo, seria possível calcular a posição e sua velocidade em qualquer outro instante de tempo. O objetivo da solução 
dessa equação será demonstrar que a conservação da energia e do momento angular são consequências das leis de Newton.
Será demonstrada na subseção a seguir.