Aulas particulares Tarefas Tira-dúvidas Planos Entrar Criar conta

Resolva suas atividades acadêmicas

Envie sua atividade e um professor resolve

Enviar atividade

K-nearest neighbors seu primeiro algoritmo de machine learni

Por: Julio R.
08 de Junho de 2016

K-nearest neighbors seu primeiro algoritmo de machine learni

Computação Linguagens de Programação Geral Geral Geral Machine Learning (Aprendizado de Máquina) Linguagens de Programação Geral Geral

Ola queridos leitores, hoje o assunto envolvera códigos, um pouco de matemática e claro machine learning. Então pode ir abrindo seus editores pois ao final do post você terá seu algoritmo prontinho para brincar.

Mas antes de tudo vamos falar um pouco sobre o que é machine learning:

Como sabemos Machine Learning é uma área da inteligência artificial que se preocupa em "ensinar" um computador a realizar uma determinada tarefa, isso é geralmente feito por meio de analise de uma quantidade grande de dados e a partir disso o algoritmo começa a identificar padrões e depois pode realizar determinadas tarefas sozinho de acordo com a necessidade.

Claro isso é só uma definição pobre do que realmente é machine learning mas o que interessa nesse artigo é o algoritmo em si não a teoria.

Um exemplo que acho bacana é o do robozinho que tem que tomar conta de uma estufa. Nessa estufa tem 3 tipos de plantas cada qual com sua características e necessidades e como sabemos no meio das plantas podem nascer matos, aquelas plantas indesejáveis, e esse robô precisa identificar o que são plantas e o que é mato, e realizar uma ação como por exemplo arrancar os matinhos, ele também precisa diferencia as 3 espécies de plantas pois elas requerem cuidados diferentes, por exemplo os remédios para parasitas e horário de serem regadas.

vemos um problema típico de machine learning que é a classificação ou seja é preciso mostrar a esse robô uma grande quantidade de imagens de plantas para que ele aprenda a identificar as plantas e os matinhos nesse processo poderemos usar alguns algoritmos um deles é o K-nearest neighbors.

clustering

Claro que na vida real fazer isso iria ser bem complexo e exigiria um pouco de trabalho, mas esse exemplo é só para ilustrar.

Por isso não tratarei aqui desse exemplo em especial.

Mas deixemos de conversa.

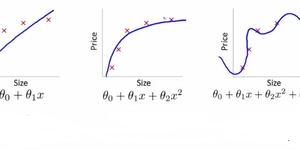
Em machine learning existem alguns tipos de problemas específicos e cada tipo de problema requer um raciocínio próprio para ser resolvido, alguns autores dizem que existem 3 problemas básicos que são: classificação, clustering(agrupar) e a regressão não irei discuti-los nesse post mas farei no futuro com certeza.

O algoritmo de hoje pode ser usado tanto na classificação quanto no clustering mas iremos usa-lo para classificar.

Antes disso

Classificar: a grosso modo seria como o próprio nome diz classificar um conjunto de dados de acordo com as características que eles tem em comum e depois etiqueta-los.

Muito bem hora de colocar a mão na massa.

A linguagem de programação que será usada é python.

Para esse algoritmo você ira precisar apenas dos seguintes módulos: csv, random, math, operator.

Creio que todos esses módulos já vem incluso no python.

Antes de tudo precisamos de dados irei utilizar dois conjuntos de dados para esse código.

O primeiro e mais importante pois será ele que será utilizado para desenvolver o algoritmo é o iris.data que pode ser adquirido aqui: http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data

Basta clicar com o botão direito do mouse e salvar como iris.data.

O segundo é uma documento csv que sera usado para sabermos se o algoritmo estar de fato funcionando em outros conjuntos de dados, ele contem dados de vários pacientes e o KNN ira dizer se o tumor é maligno ou benigno.

você pode fazer o download desses dados aqui:Tab_Compl_CNT_4T15

Vamos a nossa primeira função:


# Não esqueça de importar os seguintes módulos.
import csv
import random
import math
import operator

# Essa função ira preparar os dados para a gente.
def carregarDados(documento,divisor):
"""Essa função ira carregar
   os dados e os dividira em dois grupos o conjunto_de_treino
   e o conjunto_de_teste.
   documento: será o documento que você ira utilizar
   divisor: será a proporção
   em que você ira distribuir os dados entre os
   conjuntos no caso 67% ira para o de treino
   e o resto para teste."""

    conjunto_de_teste = []
    conjunto_de_treino = []

    # Aqui nos abrimos o documento para leitura e
    # o armazenamos na variável csv_documento
    with open(documentp,'rb') as csv_documento:

        # Usamos o modulo csv para ler este documento o que o
        # transforma em um objeto csv e logo em seguida
        # transformamos ele em uma lista
        conjunto_de_dados = list(csv.reader(csv_documento))
        #Usamos o loop para cada linha do documento que no caso é
        # uma lista de listas
        for x in range(len(conjunto_de_dados)):
            #usamos um loop em cada linha pois iremos
            #transformar os dados númericos
            #que antes estavam em str em float.
            #Repare que peguei a primeira linha de
            #conjuntos_de_dados e fui ate o
            #penúltimo item pois o último é um nome.
            for y in range(len(conjunto_de_dados[0])-1)
                #Agora substituo em conjunto_de_dados os
                #valores que antes eram
                #str por float.
                conjunto_de_dados[x][y] = float(conjunto_de_dados[x][y])
            #Aqui uso o random.random para separar os dados
            # proporcionalmente.
            if random.random() <= divisor:
                conjunto_de_treino.append(conjunto_de_dados[x])
            else:
                conjunto_de_teste.append(conjunto_de_dados[x])
    #E finalmente a função retorna duas listas de listas uma para
    #treino e outra para teste
    return conjunto_de_treino,conjunto_de_teste

Pronto agora você já pode testar essa função colocando o caminho do documento Iris.data no parâmetro documento e no divisor pode colocar o número 0.67 essa é uma boa proporção para separar o documento.

Essa função retorna dois objetos então deve ser armazenada em duas variáveis não esqueça.

Agora a próxima parte envolve o calculo da distancia euclidiana que será usada para medir a distancia de uma linha do documento a outra.

Alerta: sim temos matemática mas antes de sair correndo lembre-se que o conceito será apresentado tanto em formulas quanto em código então se não quiser ver o conceito de distancia euclidiana basta pular.

para ficar fácil de compreender vamos lembrar um pouco de quando você ainda estava no ensino médio e teve que calcular a distancia entre dois pontos.

Imagina o espaço euclidiano, a formula era bem simples alias uma das aplicações mais belas do teorema de Pitagoras.

Vamos lá: dado dois pontos no espaço $p_{1}=(x_{1},y_{1},z_{1})$ e $p_{2} = (x_{2},y_{2},z_{2})$ a distancia entre eles seria.

$d = \sqrt{(x_{2}-x_{1})^2+(y_{2}-y_{1})^2+(z_{2}-z_{1})^2}$

Porem aqui só calculamos três dimensões se você olhar o documento iris.data vai percebe que temos quatro dimensões, mas isso não é problema pois a distancia euclidiana pode ser generalizada para [latex]n[/latex] se você olhar bem percebera que o que fazemos é somar o quadrado da diferença de cada coordenada do ponto.

Então iremos usar a seguinte formula:

$d = \sqrt{\sum_{k=1}^{n}(x_{1}-x_{0})^2}$

Que nada mai é de que uma generalização da distancia Éuclidiana para n-dimensões

O código fica assim:



def distanciaEuclidiana(instancia, instancia2):
"""Essa função calcula a distancia entre duas instâncias"""
    # Aqui eu inicio o contador de distancia.
    distancia = 0
    #Aqui eu dou um range na istáncia2 com o cuidado de não pegar o
    #o ultimo elemento pois se trata de uma string.
    for x in range(len(instancia2)-1):
        #Repare que calculo a diferença de cada elemento das duas istáncias
        # e depois vou adicionando cada um a variável distancia.
        distancia += pow((float(instancia[x]) - float(instancia2[x])), 2)
    #Depois basta retorna a raiz quadrada da soma e pronto.
    return math.sqrt(distancia)

Depois que ficar pronto você vera que ele pega uma instância e calcula a distancia dela em relação a todas as instâncias de treino afim de encontrar aquelas que esta mais perto dela.

Tente entender bem essa função pois ela em conjunto com a próxima é o "core" do algoritmo.

Agora finalmente a função que pega os três vizinhos mais próximos da instância dada.


def obterVizinhos(conjunto_de_treino, instancia_de_teste, k):
"""Essa função acha os 3 vizinhos que estão mais perto de
   uma instância de teste"""
   distancias = []
    #Primeiro damos um for no conjuto_de_treino assim teremos acesso
    # a cada linha deste.
    for x in range(len(conjunto_de_treino)):
        #Aqui eu calculo a distancia da instância em relação a todas
        # as outras instancias do conjunto de teste e armazeno.
        dist_euclidiana = distanciaEuclidiana(instancia_de_teste,conjunto_de_treino[x])
        #Armazeno uma tupla na variavel distancia assim crio uma lista de tuplas
        #contendo a instância de teste e sua distancia da instância dada.
        distancias.append((conjunto_de_treino[x],dist_euclidiana))
    #Aqui nos organizamos as tuplas de modo que as que estão mais
    # ficam nos primeiros lugares.
    distancias.sort(key=operator.itemgetter(1))
    vizinhos = []
    #Aqui eu simplesmente armazeno as 3 instâncias que estão mais perto
    #dentro da variável vizinho.
    for x in range(k):
        vizinhos.append(distancias[x][0])
    # A função retorna uma lista com as 3 instâncias do conjunto de treino
    # que estão mais perto da instância dada.
    return vizinhos

Pronto agora já conseguimos achar os K vizinhos mais próximos de uma instância e assim poderemos classifica-la de acordo com a proximidade com cada vizinho e seu tipo por exemplo se a planta X esta mais próxima de duas plantas do tipo A logo ele conclui que ela é do tipo A e assim por diante com todas as outras instâncias.

Agora vamos partir para a próxima é ela que é responsável por selecionar apenas um vizinho e classifica-lo de acordo com sua proximidade com os outros.



def obterResposta(vizinhos):
"""Essa função pega uma lista de listas que é o
    que retorna da função vizinhos dentro dessa
    lista tem 3 instâncias."""
votos = {}
    #damos um for na lista para selecionar apenas o
    # ultimo elemento de cada lista dentro dela pois
    # esse é um nome.
    for x in range(len(vizinhos)):
        resposta = vizinhos[x][-1]
        if resposta in votos:
            votos[resposta] += 1
        else:
            votos[resposta] = 1
        #se você olhar na parte acima viu que ele usa um
        # dicionário onde a chave é o nome e o valor é um
        # contador de ocorrências do nome.

    # depois basta que organizamos e ela retorna a chave
    # tem mais pontos.
    votos_organizados = sorted(votos.iteritems(),key=operator.itemgetter(1),reverse=True)
    return votos_organizados[0][0]

Pronto coma função acima pegamos a lista que retorna da função obterVizinhos e selecionamos o que esta mais próximo e usamos para classificar a instância de teste em questão.

Agora iremos fazer uma função que mede a precisão de nosso algoritmo.



#Nos iremos usar uma lista para armazenar as predições.
# então essa função compara o conjunto_de_teste com as
#predições e retorna a porcentagem de acerto.
def obterPrecisao(conjunto_de_teste,predicoes):
    correto = 0
    for x in range(len(conjunto_de_teste)):
        if conjunto_de_teste[x][-1] in predicoes[x]:
            correto += 1
    return (correto/float(len(conjunto_de_teste)))*100.0

Pronto feito isso podemos ir finalmente para a parte final do algoritmo e colocar todas as funções juntas e ver se tudo deu certo.


def main():
    """essa função ira rodar o algoritmo quando invocada"""
    #Estabelecemos o divisor isso quer dizer que 67%
    #conjunto de treino.
    divisor = 0.67
    # Carregamos os documentos e suas respectivas quantidades de instâncias.
    conjunto_de_treino,conjunto_de_teste = carregarDados("iris.data")
    print 'conjunto de treino:' + repr(len(conjunto_de_treino))
    print 'conjunto de teste' + repr(len(conjunto_de_teste))

    # Criamos a variável predicoes para armazenar as predições.
    predicoes = []
    k = 3
    #Repare que ele pega cada instância do conjunto de teste
    # e compara com cada uma do conjunto de teste afim de classifica-la.
    for x in range(len(conjunto_de_teste)):
        vizinhos = obterVizinhos(conjunto_de_treino,conjunto_de_teste[x],k)
        resultado = obterResposta(vizinhos)
        predicoes.append(resultado)
    print ('  predição =' + repr(resultado)+ '  atual=' + repr(conjunto_de_teste[x][-1]))
    precisao = obterPrecisao(conjunto_de_teste,predicoes)
    print("Precisão:" + repr(precisao) + '%')

Pronto queridos leitores esse foi nosso primeiro algoritmo, depois de testa-lo e entende-lo bem você pode carregar o segundo conjunto de dados que se trata de vários exames de pessoas que possuem tumores e ele ira classifica-los em malignos ou benignos de acordo com as características dos exames.

Caso tenha algum erro na hora de testar não se acanhe deixe nos comentários que concerto o mais rápido possível.