Derivada é a taxa de variação e uma função, ou seja, y varia de acordo com x
regras:
1 - Derivada de uma consntante = 0
Resolva exercícios e atividades acadêmicas
exemplo:
y=5
y'=0
Encontre o professor particular perfeito
2 - Derivada de qualquer numero junto com o X¹ = o proprio numero
exemplo:
y= X
y'=1
y=2x
y'=2
3-Derivada de uma função onde o expoente de x > 0
O espoente que estava em cima passa multiplicando o numero embaixo e em sima subtrai menos 1
exmplo
y= 7x²
y'= 2.7.x¹
y'=14X¹
y= 15x³
y'=3.15.x²
y'=45x²
Exercicios fixação
1)A posição de uma partícula que se desloca ao longo de uma reta coordenada é dada por ![]() , com s em metros e t em segundos. Determine a velocidade e a aceleração da partícula para t = 6s.
, com s em metros e t em segundos. Determine a velocidade e a aceleração da partícula para t = 6s.
Resolução:
Sabendo que a 1º derivada do espaço e a velocidade
e a segunda derivada do espaço e a aceleração então calculando acharemos
S=(1+4t)^(1/2)
Derivada de dentro . a derivada do expoente
V= 0,5.4. [(1+4t)^(-1/2)]
como o expoente ta negativo vai pra baixo positivo
V= 2/[(1+4t)^0,5 ] observação qualquer numero elevado a 0,5 e a mesma coisa que a raiz quadrada
V= 2/[(1+4.6)^0,5]
v=2/5
V=0,4 m/s
aceleação e a segunda derivada do espaço ou a primeira derivada da velocidade
V= 0,5.4. [(1+4t)^(-1/2)]
V= 2.[(1+4t)^-0,5]
a= 2.4.-0,5.[(1+4t)^-1,5]
a= -4/[(1+4t)^1,5]
a= -4/(25^1,5)
a=-4/125
a=-0,032m/s²
2)Uma partícula se move sobre uma trajetória segundo a equação abaixo onde S é dado em metros e t em segundos. Determine a velocidade e aceleração nos valores indicados:
Determine a velocidade no instante t = 3 s
S=2t²-10t+1
Resolução:
V= 2.2t-10+0
V=4t-10
v=4.3-10 = 12-10
V= 2m/s
V=4t-10
a= 4-0
a= 4m/s²
3)Um quadrado de lado l está se expandindo segundo a equação l = 5 + t³ , onde a variável t representa o tempo. Determinar a taxa de variação da área desse quadrado quando t = 2. (I em metros, t em segundos)
Resolução:
Sabendo que para calcular a area de um quadrado todos os lados sao iguais entao I²
temos o valor de I portanto
A= I²
A= (5+t³)²
taxa de variação usa a derivada
A'= 2.3t²(5+t³)¹
sabendo que o 2 que passa multiplicando era o expoente da função
e o 3t² e a derivada de dentro da função
A'= 6t².(5+t³)
substituindo o valor de t temos:
A'= 6.2².(5+2³)
A'= 24.(5+8)
A'=24.13
A'= 312m²/s
3)Suponhamos que daqui a x meses a população de uma certa comunidade será P(x)=x²+4x+3000 habitantes. Qual é a taxa de variação da população daqui a 3 meses?
Resolução:
Ja que é taxa de variação entao tem que deriva
P'(x) = 2x+4+0 = 2x+4
substituindo o valor do mes
P'(x)=2.3+4 = 6+4 = 10hab/mes
4)Uma folha de papelão labirinto que vai ser exposta em forma de um quadrado, este labirinto deve ser feita de uma folha de papelão medindo 16 por 30 cm, destacando-se quadrados iguais dos quatro cantos e dobrando-se os lados.Qual é o tamanho dos quadrados para se obter uma caixa com o maior volume?
Resolução:
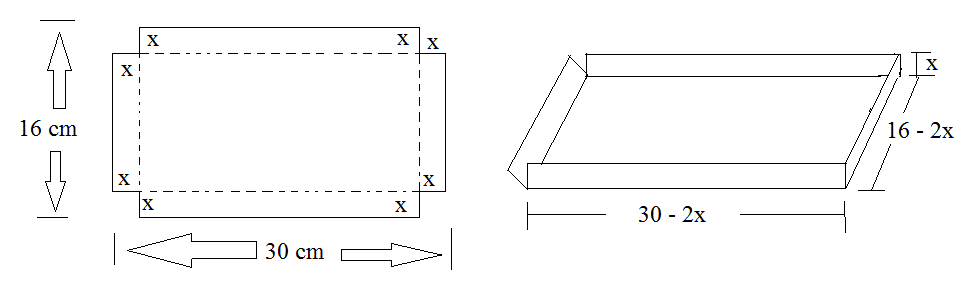
observando que na hora de dobra os lador tenho duas partes que eu irei dobrar sem saber o tamanho por isso eu coloco esse -2x
sabendo que V= B.H.L
então:V= (30-2x).(16-2x).x
V=(480-60x-32x+4x²).X
V=480x-92x²+4x³
portanto V'= 480-184x+12x²
achamos uma equação do segundo grau
usando baskara
acharemos o comprimento
sabendo que comprimento nao pode ser negativo temos
X'=12
x'=10/3
Restrições ja que uma parte do papelão tem 16cm para forma a caixa x tem que ser4 menos do que a metade desse comprimento
0<x<8
portanto o maior quadrado possivel é x=10/3
Qualquer duvida entre em contato por email : viktorgomides@hotmail.com
mande suas principais duvidas e questões que todas serão postadas aqui

