O Jogo de Monty Hall (Você trocaria ou não de porta? Ou tant

Pessoal,

 
Mostrarei um clássico problema muito intrigante e contra-intuitivo da Teoria da Probabilidade. Seu nome é o Problema de Monty Hall e na verdade é um jogo.
Esse jogo surgiu a partir de um concurso televisivo dos Estados Unidos chamado “Let’s Make a Deal”, exibido na década de 1970, cujo apresentador era o Monty Hall.
O jogo se tornou muito popular, pois na maioria dos casos os participantes tomavam a decisão errada, pois seguiam a intuição e não pensavam de forma exata.
É muito raro alguém tomar a decisão certa por ela ser tão contra-intuitiva. Para ser super sincero, eu mesmo errei quando me apresentaram a brincadeira.

Para entender o jogo, a melhor maneira é brincar!
 
Suponha que você está no programa de TV do Monty Hall. É a última fase do jogo e você está prestes a ganhar um carro!
Monty Hall te apresenta 3 portas para você escolher uma e fala que atrás de uma delas está o carro e que nas outras estão apenas bodes (prêmio ruim).

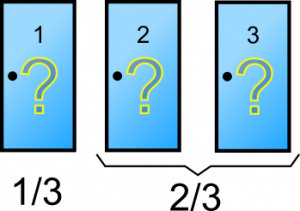
Nesse momento, qual a probabilidade de acertar a porta com o carro escolhendo qualquer uma delas? 1/3?
Exatamente! Então suponha que você escolheu a porta 1.

Monty Hall então faz uma cara triste e toma uma atitude: Sabendo em qual porta está o carro, ele abre a porta 3 para mostrar que atrás dessa porta está um bode! E te oferece outra opção, continuar com a porta 1 ou mudar para porta 2.

 
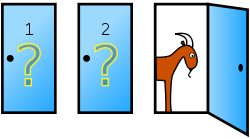
E agora? Qual é a estratégia mais lógica? Ficar com a porta escolhida inicialmente (1) ou mudar de porta? Com qual das duas portas ainda fechadas o concorrente tem mais probabilidades de ganhar? Por quê?

Bom, como sobraram apenas duas portas restantes (e apenas uma tem o carro) cada uma tem 50% de chances de ter o carro, então tanto faz mudar de porta ou continuar com a inicial, correto???

A grande maioria das pessoas tem o raciocínio apresentado acima. E a maioria por achar que “tanto faz” continua com a porta 1, pois acha que Monty Hall está pregando uma armadilha (as pessoas também se apegam a primeira escolha).
Mas esse raciocínio está completamente errado! Na verdade, trocar de porta DOBRA a sua probabilidade de ganhar o carro!

Então se você quiser dobrar suas chances de ganhar, meu caro: TROQUE DE PORTA!
 
Mas por quê??? Qual a explicação para isso?
 
Resumirei a explicação, mas também postarei um vídeo que, em minha opinião, tem a melhor explicação! O vídeo está em inglês. É possível fazer a tradução automática da legenda no YouTube, que apesar de ser bem ruim, é aconselhável para quem não entenda nada de inglês.

Segue a explicação:

Mesmo depois da revelação que a porta 3 estava aberta, a porta 1 continua com 1/3 de chances de ter o carro, e a porta 2 fica com 2/3 (o dobro).
Suponha que esse mesmo jogo seja jogado várias vezes.

Na primeira etapa, em 1/3 das vezes o jogador terá acertado o carro e em 2/3 das vezes errado. Então, na segunda etapa (com apenas duas portas), em 2/3 das vezes, se o jogador mudar de porta, ele ganhará o carro.

Para entender melhor, veja que esse jogo pode se desenrolar em três situações, imagina que o carro esteja na porta 2 e os bodes nas portas 1 e 3.

Situação 1: O jogador escolhe a porta 1. Monty Hall abre a porta 3. O jogador troca para a 2 e GANHA! Perceba que, nesse caso, Monty Hall foi obrigado a abrir a porta 3.

Situação 2: O jogador escolhe a porta 2. Monty Hall abre a porta 3. O jogador troca para a 1 e PERDE! Perceba que, nesse caso, Monty Hall poderia escolher entre as portas 1 e 3 para abrir.

Situação 3: O jogador escolhe a porta 3. Monty Hall abre a porta 1. O jogador troca para a 2 e GANHA! Perceba que, nesse caso, Monty Hall foi obrigado a abrir a porta 1.

Então, se o jogador sempre mudar de porta, em 2/3 das vezes ele ganha e em 1/3 ele perde!
Lembre-se que Monty Hall sabe que o carro está na porta 1, então ele nunca irá abrir essa porta.

Abaixo segue o melhor vídeo para visualizar e entender essa situação. Nele, entre outros métodos, é usado cartas de baralho para ilustrar de forma clara que sempre será melhor trocar de porta!

Esse problema aparece também num filme muito legal chamado “Quebrando a banca” com Kevin Spacey (2008). Super recomendo o filme! Abaixo segue o trecho do filme (achei dublado).

Espero que tenham gostado desse intrigante problema!

 
Abraços,

Felipe