TRABALHO MECÂNICO
Quando executamos uma atividade como dar aulas, estudar, capinar, dirigir, enfim, estamos trabalhando.
Dentro da Física o conceito de trabalho está ligado à força e deslocamento.
Uma força realiza trabalho quando ela desloca seu ponto de aplicação. Assim, para haver trabalho tem haver FORÇA e DESLOCAMENTO.
Numa expressão bem simples temos que : Ƭ = F.d.cosα, onde F é a intensidade da força aplicada em newtons, d o deslocamento em metros e α o ângulo que a Força faz com o deslocamento.
O mais comum é estudar a situação em que a força é paralela ao plano e, neste caso α = 0o cosα = 1, donde temos Ƭ = F.d.
UNIDADE: Newton.metro [N].[m] recebe o nome de joule [J].
Ƭ = F⋅d⋅cosα
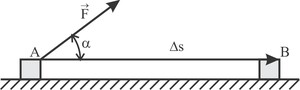d = Δs
Ƭ = trabalho realizado pela força para um deslocamento retilíneo d.
α = ângulo formado entre a força e o deslocamento retilíneo d.
TRABALHO NULO:
O Trabalho Nulo acontece em 3 (três) situações:
1a - Há força e não há deslocamento. Se d = 0 ==> F.d = 0
2a - A força e o deslocamento fazem entre si ângulo de 90o, pois cos0o = 0
3a - Há deslocamento, mas não há força. Como?
No Movimento Retilíneo Uniforme (MRU) a resultante das forças que atuam sobre um corpo é nula. Consequentemente,
neste caso o Trabalho será NULO.
OBSERVAÇÕES:
1a) O trabalho da força de atrito (Fat) sempre será negativo, pois Fat está sempre contra o sentido do deslocamento:
Ƭ(Fat) = F.d.cos(180o) ==> Ƭ(Fat) = F.d.(-1) ==> Ƭ(Fat) -= - F.d 0 ou seja Ƭ(Fat) <0 (-).
2a) O trabalho da força normal sempre será nulo, pois a força normal é sempre perpendicular à trajetória.
3a) o trabalho realizado por uma força INDEPENDE do tempo e da trajetória. Para o cálculo do trabalho é levado em conta a posição final e a posição inicial ou seja, o deslocamento.
TRABALHO DA FORÇA PESO:
Trabalho do peso
Vamos calcular o trabalho do peso de uma partícula que se desloca de um nível mais elevado (ponto A) para um nível mais baixo (ponto B), com desnível H.
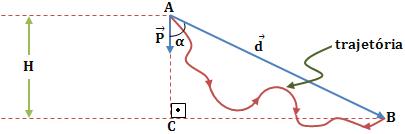
Onde:
é o peso; 
é o deslocamento de A para B.
Assim, o trabalho de peso, calculado pela definição, é dado por:
Da figura, temos:
mas, P =mg e, como demonstrado acima, |d|cosα = H
Veja que o trabalho de peso é independente da particular trajetória entre os pontos A e B
Caso o deslocamento ocorresse de modo inverso, ou seja, de B para A, o ângulo entre 
seria β = 180 – α.
Se cos β = - cos α, o trabalho de peso entre B e A é dado por:
Conclusão: na descida, o peso realiza trabalho positivo, favorecendo a queda, e na subida o peso realiza trabalho negativo, dificultando a o movimento ascendente.
Ver WhatsApp