OFICINA: CONSTRUINDO O TANGRAM E REVELANDO ALGUNS MISTÉRIOS

Tangram é um quebra-cabeça chinês formado por 7 peças (5 triângulos, 1 quadrado e 1 paralelogramo). Com essas peças podemos formar várias figuras, utilizando todas elas sem sobrepô-las. Segundo a Enciclopédia do Tangram, é possível montar mais de 1700 figuras com as 7 peças. Esse quebra-cabeça, também conhecido como jogo das sete peças, é utilizado pelos professores de matemática como instrumento facilitador da compreensão das formas geométricas. Além de facilitar o estudo da geometria, ele desenvolve a criatividade e o raciocínio lógico, que também são fundamentais para o estudo da matemática.

Objetivo:  Proporcionar ao aluno reformular conceitos apresentados de Geometria, explorando o material manipulável concreto, no nosso caso, o tangram.

Conteúdos:  Retas concorrentes e perpendiculares; conceitos de ângulos e retas; construção de polígonos; ponto médio; vértices; diagonal e figuras geométricas planas.

Metodologia:  Organizar a sala em grupos de 5 ( cinco ) alunos. Cada aluno receberá uma folha de papel oficio, de maneira que faça as dobraduras e participe das discussões entre o grupo.

Duração:  4 horas/aulas.

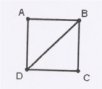
1. O aluno deve construir um quadrado a partir da folha de oficio que está com ele, além de definir os vértices, por exemplo, ABCD;

2. Feito 1, agora é solicitado que o mesmo trace uma diagonal, por exemplo, BD.

Oi! Eu sou BD!

3. Agora é possível que, diante da diagonal traçada, o professor elabore alguns questionamentos:

3.1 O que representa o segmento BD que vocês acabaram de traçar no quadrado?

3.2 E o segmento AC?

3.3 Defina diagonal do quadrado: 

3.4 O que se pode concluir sobre as diagonais AC e BD ?

Portanto, é possível elaborar questões, baseadas em conhecimentos relacionados a Geometria envolvida nas figuras que os alunos estarão encontrando ao longo da construção.

Agora o aluno precisa seguir a sequência que constrói o tangram.

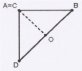
4. Determinada a diagonal BD, precisamos encontrar o ponto médio, que aqui chamaremos de O, e fazer com que o aluno reconheça que este divide o segmento BD ao meio.

5. Na sequência, ao determinar o ponto médio de BD, o ponto O, será pedido que o mesmo ligue o ponto O ao ponto A. Como podemos ver na figura abaixo.

5.1 Que figura é essa?

6. Agora, dobre a figura sobre o segmento AO e em seguida, dobre o papel de modo que o vértice C coincida com o ponto O. Observe que surgiram outros triângulos.

6.1 Qual é a característica em comum, para os triângulos, em relação ao ponto O?

7. Nesse ponto, a fim de fazer com que o aluno sempre retome o início da construção, o professor pode novamente elaborar perguntas sobre o quadrado que originou toda a construção até o ponto onde o mesmo se encontra.

7.1 Voltando ao quadrado, o que se pode concluir sobre as retas suportes de suas diagonais?

7.a Fica a cargo do professor a elaboração antecipada do questionário que quer desenvolver com a turma, nos pontos de construção do tangram.

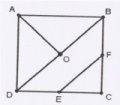
8. Retomando a construção, dobre o quadrado de modo que o vértice C coincida com o ponto O. Marque e nomeie o segmento obtido como sendo EF.

8.2  Nesse momento, o aluno pode observar as diversas figuras que já determinaram até então.

8.3 Só para relembrar:

8.3.1 Um quadrado ABCD, três triângulos AOB, AOD e ECF, além de um figura DEFBD que eles nada poderão concluir ainda.

Estamos quase lá! Vamos agora para mais uma manipulação com o papel.

9. Pegue o vértice D e vá até o ponto O, de modo que coincida com O.

Obtemos, com essa dobra, um segmento que chamaremos de G, como segue na figura abaixo.

10. Prolongue o segmento AO até encontrar EF, como na figura abaixo, e nomeie este de H.

Bem, estamos no final e… para completar, e encontrarmos as duas últimas peças deste quebra-cabeça… tchan ran!

11. Dobre o segmento BC de modo que o ponto F coincida com o ponto O e o segmento FH, com o segmento OH. Assim, oh!

E finalizamos o nosso tão famoso tangram, embora ainda desconhecido por muitos… mas acredito que, desta vez, não mais

Bem, tirando toda a parte divertida ( não tio, não tio! ), é evidente que esse trabalho desenvolvido com os alunos torna muito mais fácil de assimilar tantos conhecimentos, além de, voltando à parte divertida, ser mesmo muito divertido para eles toda essa manipulação com o papel, suas dobras, encontros das figuras, enfim, toda a geometria, antes “pesada” para a grande maioria, torna-se muito mais “leve”, mais compreensível.

Ressaltando que, o professor deve escolher as questões, e a maneira como dividirá a sala, de forma que o desenvolvimento da atividade não se torne algo desanimador para o aluno e incontrolável para quem está aplicando.

Bem, é isso e… Até a próxima!