A teoria sociocultural de aprendizagem de Vygotsky

Piaget possibilitou nos concentrarmos sobre a atividade cognitiva da criança e começar a compreender como um indivíduo usa ideias de maneira reflexiva para construir e compreender novo conhecimento. Vygotsky abordou a interação social como um componente essencial no desenvolvimento do conhecimento. Ele acreditou que existem processos mentais entre as pessoas em ambientes de aprendizagem social e que nesses ambientes, o estudante desenvolve ideias para seu próprio mundo psicológico. Essa transferência das ideias externas ao indivíduo – compartilhadas no ambiente social – para aquelas que são constructos pessoais internos Vygotsky chamou internalização. A internalização só ocorre dentro da zona de desenvolvimento proximal de cada estudante (ZDP)”. A ZDP não é um espaço físico, mas um espaço simbólico criado pela interação dos estudantes com outros mais instruídos e com a cultura que os precede” (Goos, 2004, p. 262).

Para melhor compreender o conceito da ZDP, considere que Vygotsky concebeu as ideias que existem na sala de aula, nos livros e aquelas compartilhadas por professores e outras autoridades como distintas das ideias construídas pela criança. Ele chamou as ideias bem-formuladas e externas à criança de conceitos científicos, enquanto aquelas desenvolvidas pela criança (da maneira descrita por Piaget) ele chamou de conceitos espontâneos.

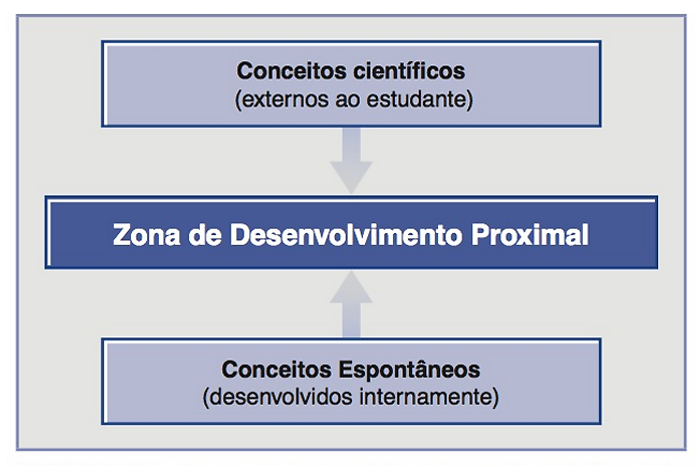
Vygotsky fala sobre esses dois tipos de conceitos funcionando em sentidos opostos, como ilustrado na Figura abaixo. Os conceitos científicos funcionam para baixo a partir de uma autoridade externa. Como tal, eles impõem sua lógica sobre a criança. Os conceitos espontâneos borbulham para cima, como resultado da atividade reflexiva da criança. Na ZDP de Vygotsky, a criança é capaz de trabalhar significativamente com os conceitos científicos externos, incluindo aqueles das discussões em sala de aula. Aqui a própria compreensão conceitual da criança está suficientemente avançada para começar a retirar as ideias de “cima” dela.

Não é necessário escolher entre uma teoria socioconstrutivista que favoreça as visões de Vygotsky ou um construtivis- mo cognitivo construído com base nas teorias de Piaget (Cobb, 1996). Em uma comunidade de aprendizes de matemática, a aprendizagem dos estudantes é ampliada pelo pensamento reflexivo que a interação social promove. Ao mesmo tempo, o valor da interação social para os estudantes individuais é determinado em grande medida pelas ideias que cada indivíduo traz às discussões. Quando a conversação da sala de aula está dentro da ZDP de qualquer determinada criança, a melhor aprendizagem social acontecerá. As discussões em sala de aula baseadas nas próprias ideias e soluções para os problemas são absolutamente “fundamentais à aprendizagem das crianças” (Wood e Turner-Vorbeck, 2001, p. 186).

Goos (2004) aponta que as interpretações iniciais da ZDP de Vygotsky conduziram à noção de andaime* na qual os professores e tutores auxiliam os estudantes na resolução de problemas que eles poderiam não resolver por sua própria conta. Esse conceito de "andaime" ou de apoio, ainda popular hoje, sugere mais uma abordagem de transferência de conhecimento para a aprendizagem do que uma compreensão da internalização de Vygotsky. Cobb e Goos sugerem que em uma visão mais atual da ZDP, o conhecimento não é transmitido. Em vez disso, em uma verdadeira comunidade de aprendizes de matemática existe algo como uma ZDP comum que emerge entre os estudantes além das ZDPs individuais dos estudantes. A aprendizagem, até mesmo quando vista de um ponto de vista construtivista, ocorre e é ampliada quando os estudantes se envolvem e se engajam na cultura social de uma comunidade de aprendizes de matemática.