O que é distribuição t de Student?

Entenda rapidamente os conceitos de distribuição t de Student e o porque da sua utilização.

Estatística Ensino Médio Ensino Fundamental Geral Ensino superior Vestibular Profissional ENEM Probabilidade Inferência Probabilidade e Estatística Distribuições De Probabilidade

Para amostras pequenas (n ≤ 30), a distribuição Normal apresenta valores menos precisos, o que nos leva a utilizar um modelo melhor, a Distribuição t de Student, proposta pelo pesquisador Willian Gosset em 1908.

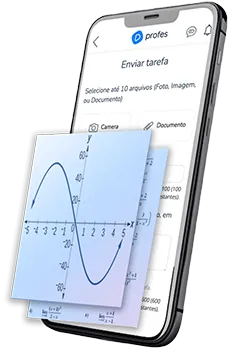
A distribuição t também tem a forma normal e é simétrica sobre a média. A principal diferença é que a distribuição t tem mais áreas nas caudas, fazendo com que seus valores críticos sejam maiores que os da distribuição Normal. Como consequência, o intervalo de confiança usando a distribuição t ficará mais largo se usa-se a distribuição Normal. A idéia aqui é que você deve pagar um preço por trabalhar com pequenas amostras.

Cada tamanho amostral possui sua própria distribuição t, ou seja, ao contrário da distribuição normal, a distribuição t não tem forma fixa, mas sim uma família de curvas. Cada curva é determinada por um parâmetro chamado grau de liberdade, encontrado pelo tamanho da amostra menos um (GL = n - 1). A idéia aqui é que o preço a ser pago por se ter uma amostra muito pequena, como 5, é mais alto do que o preço por se ter uma amostra de tamanho um pouco maior, como 10 ou 20.

O grau de liberdade se refere ao número de valores que são livres para variar após estabelecerem algumas restrições de dados.

Por exemplo, se uma amostra de tamanho 4 produz uma média de 87, sabemos que a soma dos números é 4 * 87 = 348; isso não diz nada sobre os valores individuais da amostra – há números infinitos de formas para se obter 4 números que somem 348; mas quando escolhemos três deles, o quarto é determinado. O primeiro número pode ser 84, o segundo 98 e o terceiro 81, então o quarto tem de ser 85, o único número que produzirá a média amostral conhecida, ou seja, existe n - 1 ou 3 graus de liberdade nesse exemplo.

Conforme os graus de liberdade aumentam, a distribuição t se aproxima da distribuição normal. Depois de 30 gl, a distribuição t está muito próxima à distribuição normal.

Para saber mais leia este artigo e também o meu livro acadêmico (ver pág 66).

Um abraço!

Prof MSc Uanderson Rebula