Pitágoras (c.569 - c.480 a.C.) nasceu na ilha de Samos, perto de Mileto onde 50 anos antes tinha nascido Tales. Foi a partir das ideias desses dois grandes personagens que a Matemática se inicia como ciência e pôde se desenvolver enormemente nos séculos seguintes.

Pitágoras viajou bastante. Esteve no Egito e na Babilônia (Suspeita-se que tenha ido até a Índia) onde conseguiu os conhecimentos matemáticos e as ideias religiosas de cada região. Voltando ao mundo grego, fundou em crotona (Sudeste da Itália de hoje) uma escola, que na verdade era uma sociedade secreta dedicada ao estudo da matemática e filosofia, principalmente. Como tudo o que era documento da época foi-se perdido, o que se sabe sobre o assunto veio de referências de autores que viveram séculos depois. Por este motivo que Pitágoras é ainda uma personagem obscura na história matemática e, para dificultar ainda mais as coisas, a sua escola além de ser secreta era comunitária, ou seja, todos os conhecimentos e descobertas eram comuns, pertenciam a todos. Assim não há hipóteses de saber se realmente foi Pitágoras quem descobriu o teorema que leva o seu nome, pois na época era-se muito comum dar todo o crédito de uma descoberta ao seu mestre.

Não se tem certeza qual foi a demonstração usada originalmente por Pitágoras, mas suspeita-se de ser alguma envolvendo áreas.

Desde o século 5 a.C. até 20 d.C. diversas demonstrações do Teorema de Pitágoras apareceram. No ano de 1940 o Matemático americano E.S. Loomis publicou 370 demonstrações diferentes, mas ainda existem mais!

Antes de Pitágoras

Na Babilônia

Existem provas concretas de que os babilônios já conheciam o Teorema de Pitágoras. Diversos tabletes de barro que datam do período de 1800 a 1600 a.C. foram encontrados, decifrados e hoje podem ser vistos em diversos museus. Um dos tabletes, chamado Plimpton 322 está na Universidade de Columbia e o fragmento que está preservado mostra-nos uma tabela de 15 linhas e 3 colunas de números. Pesquisadores concluíram que esta tabela é uma tabela de ternos pitagóricos, ou seja, uma tabela com os lados de um triângulo retângulo. Como o que se encontrou era apenas um pedaço de um conjunto de tabletes, não se sabe como foram encontrados estes números. Mas a pista que deixa muito evidente o conhecimento do teorema pelos babilônios está em um tablete, que hoje se encontra no Museu Britânico. No tablete está escrito o seguinte:

4 é o comprimento
5 é a diagonal
Qual é a altura?
4 vezes 4 dá 16
5 vezes 5 dá 25
Tirando 16 de 25 dá 9
Quantas vezes quanto devo tomar para ter 9?
3 vezes 3 dá 9
3 é a altura

Isto nos mostra que certamente os babilônios tinham o conhecimento da relação entre os lados de um triângulo retângulo. Obviamente não há nenhuma prova para o teorema, pois os matemáticos da época ainda não preocupavam com isto. Eles tinham receitas que funcionavam, e com essas receitas eles resolviam problemas.

Um outro tablete que merece nossa atenção se encontra no museu da Universidade de Yale. É o único que nos fornece figuras, um quadrado e suas diagonais. Neste fragmento o lado do quadrado foi tomado como 30 e o comprimento da diagonal aparece como 42, 25, 35.

Como os babilônios escreviam os números em base 60, o comprimento da diagonal é, na nossa notação decimal, 42 + 25/60 + 35/3600 = 42,4263889. Se dividirmos este resultado por 30, obtemos o valor 1,414213..., que é uma excelente aproximação de √2, com 6 casas decimais corretas.

Na China

O Teorema de Pitágoras já era de conhecimento dos chineses 600 anos antes do que Pitágoras.

Um famoso livro chinês, o Zhoubi Suanjing do século 3 a.C. reuniu 246 problemas muito antigos, onde um deles era o "Gou Gu", o equivalente chinês do Teorema de Pitágoras que se vê na figura a seguir.

Se for bem observada, esta figura apresenta uma demonstração do Teorema usando áreas. Estudiosos acreditam que esta figura apresentada várias vezes durante os séculos, seja da Dinastia Han, cerca de 1100 anos a.C. É de certeza que nenhum artigo chinês da antiguidade chegou ao ocidente, logo pode-se afirmar que dois povos distintos descobriram o mesmo teorema com apenas alguns séculos de diferença.

O Enunciado do Teorema de Pitágoras

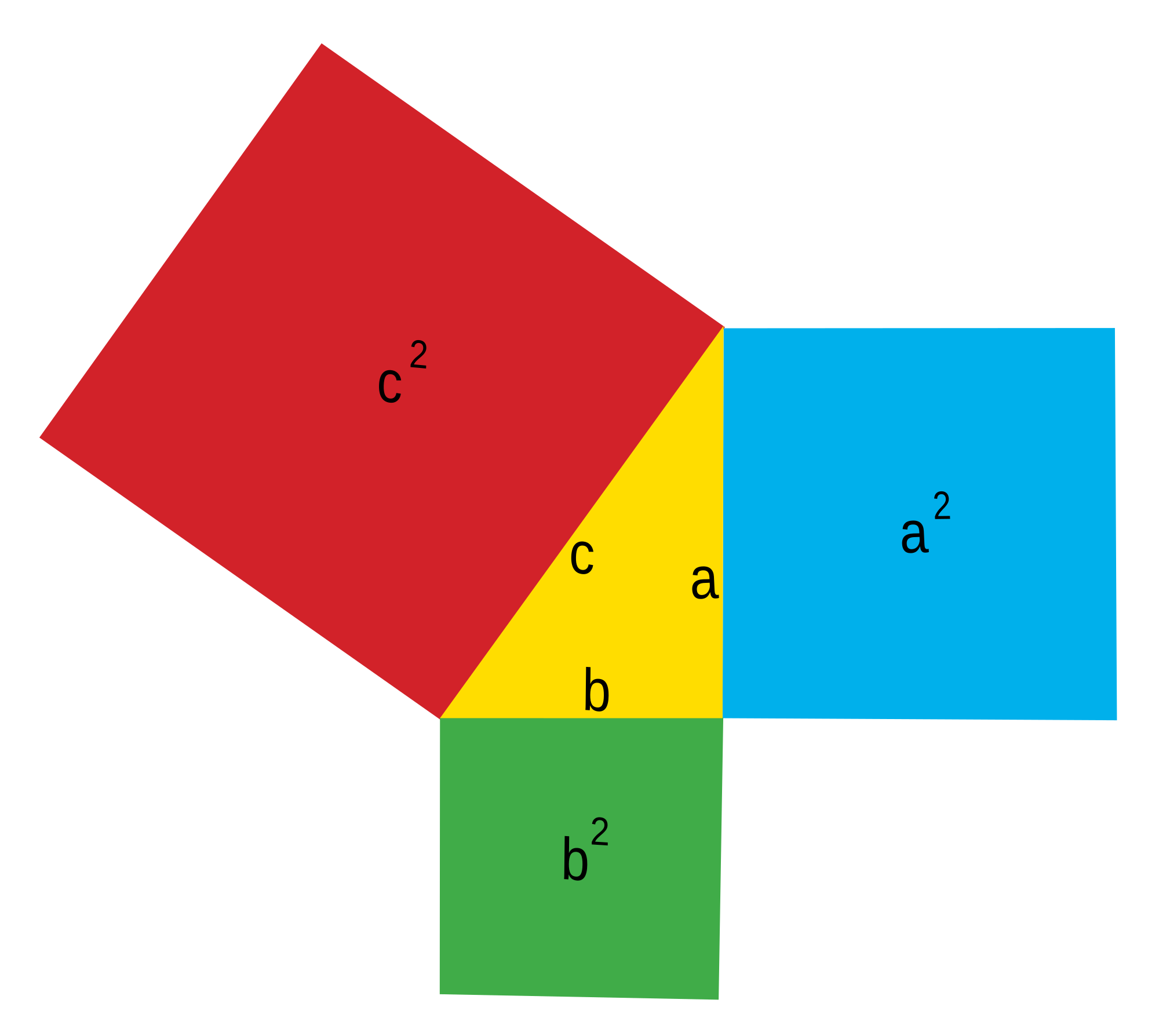
"Em qualquer triângulo retângulo, a área do quadrado cujo lado é a hipotenusa é igual à soma das áreas dos quadrados que têm como lados cada um dos catetos."

Se a é a medida da hipotenusa, e se b e c são as medidas dos catetos, o enunciado do Teorema de Pitágoras equivale a afirmar que:

a²=b²+c²

O Teorema nos diz que a área mais sombreada mais clara da figura é igual a área sombreada mais escura. Este fato não é tão evidente, intriga ainda muitas pessoas que o conhecem pela primeira vez.

A Demonstração Clássica

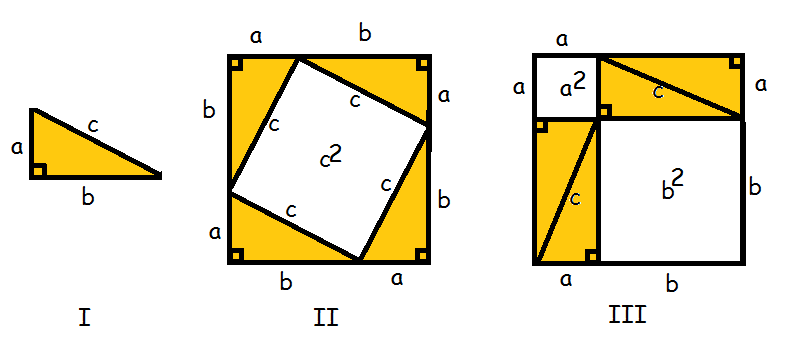
Dado um triângulo retângulo de hipotenusa a e catetos b e c, considere o quadrado cujo lado é b + c.

Na figura da esquerda, retiramos do quadrado de lado b + c quatro triângulos iguais ao dado, restando um quadrado de lado a. Na figura da direita, retiramos também do quadrado de lado b + c os quatro triângulos iguais ao dado, restando um quadrado de lado b e um quadrado de lado c. Logo a área do quadrado de lado a é igual a soma das áreas dos quadrados cujos lados medem b e c

Pode ser esta a simples e formidável demonstração que Pitágoras e seus seguidores imaginaram.

Da semelhança de triângulos AHC e ABC temos b²= am e da semelhança dos triangulos AHB e ABC temos c²= an. Somando essas duas relações membro a membro, encontramos:

b²+c²= am + an = a(m+n) = a.a =a²

Encontramos frequentemente este tipo de demonstrações nas escolas, pois além de ser uma interessante demonstração do Teorema de Pitágoras, ela inscita o desenvolvimento das relações importantes do triângulo retângulo. Além das duas que encontramos no início da demonstração, conseguimos obter também bc = ah, que também se interpreta com conceito de área, e h2= mnque nos mostra o fato importante de que a altura é a média geométrica entre as projeções dos catetos sobre a hipotenusa.

A Demonstração de Perigal

Em 1873, Henry Perigal que era um livreiro em Londres, publicou a demonstração da figura abaixo. É a forma mais evidente de perceber que a soma das áreas dos quadrados construídos sobre os catetos preenchem o quadrado construído sobre a hipotenusa.

Henry corta o quadrado construído sobre o maior cateto por duas retas passando pelo seu centro, uma paralela à hipotenusa do triângulo e outra perpendicular, dividindo este quadrado em 4 partes congruentes. Estas 4 partes mais o quadrado construído sobre o menor cateto preenchem por completo o quadrado construído sobre a hipotenusa. É necessário entretanto, provar que a região que fica no interior do quadrado maior é realmente congruente com o quadrado menor.