Olá pessoal, tudo bem com vocês?
No artigo de hoje resolveremos alguns limites bem legais. Limites são objetos dentro de uma área da matemática conhecida como "Cálculo". E são esses que iremos resolver:
- \lim_{x \to -3} \frac{x^4 - 81}{x^2 - 9}
- \lim_{x \to \infty} \frac{9x^4 - 3x^3 - 2x - 3}{-3x^4 + 5x + 21}
- \lim_{x \to \infty} \frac{9x^4 - 3x^3 - 2x - 3}{-3x^5 + 5x + 21}
- \lim_{x \to 0} \frac{-7x + 2}{3x - 5} \cdot \frac{\sin 3x}{4x}
- \lim_{x \to 0} \cos \left( \frac{2x^3}{x^2 + 3} \right) \cdot \frac{5}{2x+7}
a) 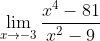
Esse limite inicialmente resulta numa indeterminação do tipo , pois substituir
na expressão do limite anula tanto o numerador (o que não seria um problema) quanto o denominador (esse sim é um problema). Então, primeiro precisamos eliminá-la do limite.
Resolva exercícios e atividades acadêmicas
A sacada aqui é perceber qeu o numerador é uma diferença de quadrados entre e
:
A diferença entre os quadrados de quaisquer dois reais e
é:
Encontre o professor particular perfeito
Nesse caso, ,
,
e
Então, o numerador do limite pode ser fatorado para:
Essa expressão permite simplificar o limite e eliminar sua indeterminação:
O novo limite é simples e não possui indeterminação, portanto podemos calculá-lo:
b) 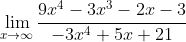
Esse limite possui uma indeterminação do tipo , pois tanto o numerador quanto o numerador crescem indefinidamente quando
tende a infinito.
Para eliminar a indeterminação e calcular o limite, fatoramos o numerador e o denominador, colocando em evidência o termo de maior grau de cada um:
Substituindo os polinômios do numerador e denominador do limite pelas suas formas fatoradas, temos o seguinte novo limite:
O limite é uma operação linear, ou seja, o limite da soma é a soma dos limites. Por isso, cada termo dentro dos parênteses no numerador e denominador tende a zero quando tende a infinito. O limite pode então ser simplificado para:
O limite ainda contém a mesma indeterminação, mas o termo no numerador e denominador pode ser cancelado. Portanto:
c) 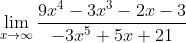
Esse limite é similar ao anterior, com a única diferença de que o termo de maior grau no denominador é agora .
Os passos são os mesmos do exemplo anterior. O limite simplificado possui a seguinte forma:
Esse limite nada mais é que o limite da função multiplicada pela constante
. O limite de
para
tendendo a infinito é zero:
d) 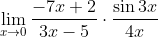
...
\lim_{u \to 0} \frac{\sin u}{u} = 1
...
u \approx 0 \Rightarrow \sin u = u
...
...



